
【題目】如圖1,點D為△ABC邊BC的延長線上一點.

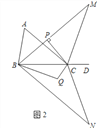
(1)若∠A∶∠ABC=3∶4,∠ACD=140°,求∠A的度數;
(2)若∠ABC的角平分線與∠ACD的角平分線交于點M,過點C作CP⊥BM于點P.
求證: ![]() ;
;
(3)在(2)的條件下,將△MBC以直線BC為對稱軸翻折得到△NBC,∠NBC的角平分線與∠NCB的角平分線交于點Q(如圖2),試探究∠BQC與∠A有怎樣的數量關系,請寫出你的猜想并證明.
【答案】(1)60°°;
(2)證明見解析;
(3)∠BQC=90°+![]() ∠A,理由見解析.
∠A,理由見解析.
【解析】試題分析:(1)先根據∠A:∠ABC=3:4,設∠A=3k,∠ABC=4k,再由三角形外角的性質求出k的值,進而可得出結論;
(2)根據三角形外角的性質得出∠M=∠MCD-∠MBC,∠A=∠ACD-∠ABC.再由MC、MB分別平分∠ACD、∠ABC得出![]() ,
, ![]() ,
,
故![]() ,根據CP⊥BM即可得出結論;
,根據CP⊥BM即可得出結論;
(3)根據BQ平分∠CBN,CQ平分∠BCN可知![]() ,
, ![]() ,再根據三角形內角和定理可知,
,再根據三角形內角和定理可知, ![]() ,根據軸對稱性質知:
,根據軸對稱性質知:
∠M=∠N,由此可得出結論.
(1)解:∵![]() ,∴可設
,∴可設![]() .
.
又∵![]()
![]() °,
°,
∴![]() °,
°,
解得 ![]() °.
°.
∴![]() °.
°.
(2)證明:
![]()
(3)猜想∠BQC=90°+![]() ∠A.
∠A.
證明如下: ∵BQ平分∠CBN,CQ平分∠BCN,
∴![]() ,
,
∴![]()
![]()
![]() .
.
由(2)知: ![]() ,又由軸對稱性質知:∠M=∠N,
,又由軸對稱性質知:∠M=∠N,
∴![]() .
.
本題考查了三角形的內角和,三角形外角的性質,折疊的性質.(1)見比設參,然后根據外角的性質求解;(2)結合角平分線和外角的性質求解;(2)根據軸對稱的性質和(2)的結論求解.


 習題精選系列答案
習題精選系列答案科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系上有點A(1.O),點A第一次跳動至點A1(-1,1).第四次向右跳動5個單位至點A4(3,2),…,依此規律跳動下去,點A第100次跳動至點A100的坐標是( )

A. (50,49) B. (51, 49) C. (50, 50) D. (51, 50)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖①,△ABC與△CDE是等腰直角三角形,直角邊AC、CD在同一條直線上,點M、N分別是斜邊AB、DE的中點,點P為AD的中點,連接AE、BD.
(1)猜想PM與PN的數量關系及位置關系,請直接寫出結論;
(2)現將圖①中的△CDE繞著點C順時針旋轉α(0°<α<90°),得到圖②,AE與MP、BD分別交于點G、H.請判斷(1)中的結論是否成立?若成立,請證明;若不成立,請說明理由;
(3)若圖②中的等腰直角三角形變成直角三角形,使BC=kAC,CD=kCE,如圖③,寫出PM與PN的數量關系,并加以證明.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,長方形ABCD中,AB=8,AD=4.點Q與點P同時從點A出發,點Q以每秒1個單位的速度沿A→D→C→B的方向運動,點P以每秒3個單位的速度沿A→B→C→D的方向運動,當P,Q兩點相遇時,它們同時停止運動.設Q點運動的時間為x(秒),在整個運動過程中,當△APQ為直角三角形時,則相應的x的值或取值范圍是_______________.
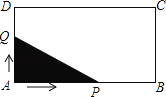
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀下列材料:
我們知道![]() 的幾何意義是在數軸上數
的幾何意義是在數軸上數![]() 對應的點與原點的距離,即
對應的點與原點的距離,即![]() =
=![]() ,也就是說,
,也就是說,![]() 表示在數軸上數
表示在數軸上數![]() 與數0對應的點之間的距離;這個結論可以推廣為
與數0對應的點之間的距離;這個結論可以推廣為![]() 表示在數軸上數
表示在數軸上數![]() 與數
與數![]() 對應的點之間的距離;
對應的點之間的距離;
例1.解方程|![]() |=2.因為在數軸上到原點的距離為2的點對應的數為
|=2.因為在數軸上到原點的距離為2的點對應的數為![]() ,所以方程|
,所以方程|![]() |=2的解為
|=2的解為![]() .
.
例2.解不等式|![]() -1|>2.在數軸上找出|
-1|>2.在數軸上找出|![]() -1|=2的解(如圖),因為在數軸上到1對應的點的距離等于2的點對應的數為-1或3,所以方程|
-1|=2的解(如圖),因為在數軸上到1對應的點的距離等于2的點對應的數為-1或3,所以方程|![]() -1|=2的解為
-1|=2的解為![]() =-1或
=-1或![]() =3,因此不等式|
=3,因此不等式|![]() -1|>2的解集為
-1|>2的解集為![]() <-1或
<-1或![]() >3.
>3.
![]()
例3.解方程|![]() -1|+|
-1|+|![]() +2|=5.由絕對值的幾何意義知,該方程就是求在數軸上到1和-2對應的點的距離之和等于5的點對應的
+2|=5.由絕對值的幾何意義知,該方程就是求在數軸上到1和-2對應的點的距離之和等于5的點對應的![]() 的值.因為在數軸上1和-2對應的點的距離為3(如圖),滿足方程的
的值.因為在數軸上1和-2對應的點的距離為3(如圖),滿足方程的![]() 對應的點在1的右邊或-2的左邊.若
對應的點在1的右邊或-2的左邊.若![]() 對應的點在1的右邊,可得
對應的點在1的右邊,可得![]() =2;若
=2;若![]() 對應的點在-2的左邊,可得
對應的點在-2的左邊,可得![]() =-3,因此方程|
=-3,因此方程|![]() -1|+|
-1|+|![]() +2|=5的解是
+2|=5的解是![]() =2或
=2或![]() =-3.
=-3.
![]()
參考閱讀材料,解答下列問題:
(1)方程|![]() +3|=4的解為 ;
+3|=4的解為 ;
(2)解不等式:|![]() -3|≥5;
-3|≥5;
(3)解不等式:|![]() -3|+|
-3|+|![]() +4|≥9
+4|≥9
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,以x=1為對稱軸的拋物線y=ax2+bx+c的圖象與x軸交于點A,點B(﹣1,0),與y軸交于點C(0,4),作直線AC.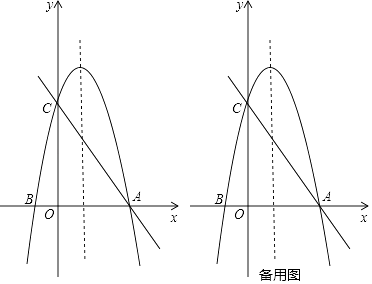
(1)求拋物線解析式;
(2)點P在拋物線的對稱軸上,且到直線AC和x軸的距離相等,設點P的縱坐標為m,求m的值;
(3)點M在y軸上且位于點C上方,點N在直線AC上,點Q為第一象限內拋物線上一點,若以點C、M、N、Q為頂點的四邊形是菱形,請直接寫出點Q的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
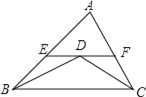
【題目】如圖,△ABC中,BD平分∠ABC,CD平分∠ACB,過點D作EF∥BC,與AB、AC分別相交于E、F,若已知AB=9,AC=7,求△AEF的周長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】首條貫通絲綢之路經濟帶的高鐵線﹣寶蘭客專進入全線拉通試驗階段,寶蘭客專的通車對加快西北地區與“一帶一路”沿線國家和地區的經貿合作、人文交流具有十分重要的意義.試運行期間,一列動車從西安開往西寧,一列普通列車從西寧開往西安,兩車同時出發,設普通列車行駛的時間為x(小時),兩車之間的距離為y(千米),圖中的折線表示y與x之間的函數關系,根據圖象進行一下探究:
【信息讀取】
(1)西寧到西安兩地相距 千米,兩車出發后 小時相遇;
(2)普通列車到達終點共需 小時,普通列車的速度是 千米/小時.
【解決問題】
(3)求動車的速度;
(4)普通列車行駛t小時后,動車到達終點西寧,求此時普通列車還需行駛多少千米到達西安?

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知△ABC是等邊三角形,點D、F分別在線段BC、AB上,∠EFB=60°,DC=EF.
(1)求證:四邊形EFCD是平行四邊形;
(2)若BF=EF,求證:AE=AD.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com