
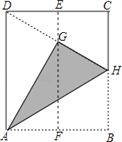
【題目】如圖,在一張矩形紙片ABCD中,AD=4cm,點E,F分別是CD和AB的中點,現將這張紙片折疊,使點B落在EF上的點G處,折痕為AH,若HG延長線恰好經過點D,則CD的長為_________.
【答案】![]()
【解析】試題分析:先證明EG是△DCH的中位線,繼而得出DG=HG,然后證明△ADG≌△AHG,得出∠BAH=∠HAG=∠DAG=30°,在Rt△ABH中,可求出AB,也即是CD的長.
試題解析:∵點E,F分別是CD和AB的中點,
∴EF⊥AB,
∴EF∥BC,
∴EG是△DCH的中位線,
∴DG=HG,
由折疊的性質可得:∠AGH=∠ABH=90°,
∴∠AGH=∠AGD=90°,
在△AGH和△AGD中,
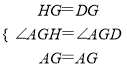
∴△ADG≌△AHG(SAS),
∴AD=AH,∠DAG=∠HAG,
由折疊的性質可得:∠BAH=∠HAG,
∴∠BAH=∠HAG=∠DAG=![]() ∠BAD=30°,
∠BAD=30°,
在Rt△ABH中,AH=AD=4,∠BAH=30°,
∴HB=2,AB=2![]() ,
,
∴CD=AB=2![]() .
.


科目:初中數學 來源: 題型:
【題目】如圖所示,PA,PB是⊙O的兩條切線,A,B為切點,連接PO,交⊙O于點D,交AB于點C,
(1)寫出圓中所有的垂直的關系;
(2)若PA=4,PD=2,求半徑OA的長;

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在Rt△ABC中,∠BAC=90°,∠B=60°,△ADE可以由△ABC繞點 A順時針旋轉900得到,點D 與點B是對應點,點E與點C是對應點,連接CE,則∠CED的度數是( )

A. 45° B. 30° C. 25° D. 15°
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:如圖,線段![]() 和射線
和射線![]() 交于點
交于點![]() .
.
(![]() )利用尺規完成以下作圖,并保留作圖痕跡(不寫作法).
)利用尺規完成以下作圖,并保留作圖痕跡(不寫作法).
①在射線![]() 上作一點
上作一點![]() ,使
,使![]() ,連接
,連接![]() ;
;
②作![]() 的角平分線交
的角平分線交![]() 于
于![]() 點;
點;
③在射線![]() 上作一點
上作一點![]() ,使
,使![]() ,連接
,連接![]() .
.
(![]() )在(
)在(![]() )所作的圖形中,通過觀察和測量可以發現
)所作的圖形中,通過觀察和測量可以發現![]() ,請將下面的證明過程補充完整.
,請將下面的證明過程補充完整.

證明:∵![]() ,
,
∴![]() __________
__________![]() __________,①
__________,①
∵![]() 平分
平分![]() ,
,
∴![]() ,
,
∴![]() __________,②
__________,②
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .( )
.( )
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】要從甲.乙兩名同學中選出一名,代表班級參加射擊比賽,如圖是兩人最近10次射擊訓練成績的折線統計圖.
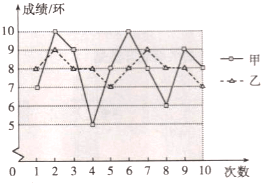
(1)已求得甲的平均成績為8環,求乙的平均成績;
(2)觀察圖形,直接寫出甲,乙這10次射擊成績的方差![]() ,
, ![]() 哪個大;
哪個大;
(3)如果其他班級參賽選手的射擊成績都在7環左右,本班應該選 參賽更合適;如果其他班級參賽選手的射擊成績都在9環左右,本班應該選 參賽更合適.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】八年2班組織了一次經典誦讀比賽,甲乙兩組各10人的比賽成績如下表(10分制):

(I)甲組數據的中位數是 ,乙組數據的眾數是 ;
(Ⅱ)計算乙組數據的平均數和方差;
(Ⅲ)已知甲組數據的方差是1.4分2,則成績較為整齊的是 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,學校準備在教學樓后面搭建一簡易矩形自行車車棚,一邊利用教學樓的后墻(可利用的墻長為19m),另外三邊利用學校現有總長38m的鐵欄圍成。
(1)若圍成的面積為180m2,試求出自行車車棚的長和寬;
(2)能圍成的面積為200m2自行車車棚嗎?如果能,請你給出設計方案;如果不能,請說明理由。

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,等腰Rt△ABC(∠ACB=90°)的直角邊與正方形DEFG的邊長均為2,且AC與DE在同一直線上,開始時點C與點D重合,讓△ABC沿這條直線向右平移,直到點A與點E重合為止.設CD的長為x,△ABC與正方形DEFG重合部分(圖中陰影部分)的面積為y,則y與x之間的函數關系的圖象大致是( )

A.  B.
B. 
C.  D.
D. 
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com