
【題目】如圖,AB是⊙O的直徑,BD是⊙O的弦,延長BD到點C,使DC=BD,連接AC,E為AC上一點,直線ED與AB延長線交于點F,若∠CDE=∠DAC,AC=12.
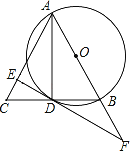
(1)求⊙O半徑;
(2)求證:DE為⊙O的切線;
【答案】(1)半徑為6;(2)見解析
【解析】
(1)根據直徑所對的圓周角是直角,證明AD⊥BC,結合DC=BD可得AB=AC=12,則半徑可求出;
(2)連接OD,先證得∠AED=90°,根據三角形中位線定理得出OD∥AC,由平行線的性質,得出OD⊥DE,則結論得證.
解:(1)∵AB為⊙O的直徑,
∴∠ADB=90°,
∴AD⊥BC,
又∵BD=CD,
∴AB=AC=12,
∴⊙O半徑為6;
(2)證明:連接OD,
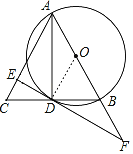
∵∠CDE=∠DAC,
∴∠CDE+∠ADE=∠DAC+∠ADE,
∴∠AED=∠ADB,
由(1)知∠ADB=90°,
∴∠AED=90°,
∵DC=BD,OA=OB,
∴OD∥AC.
∴∠ODF=∠AED=90°,
∴半徑OD⊥EF.
∴DE為⊙O的切線.


科目:初中數學 來源: 題型:
【題目】如圖,△ABC中,P'是邊AB上一點,四邊形P'Q'M'N'是正方形,點Q',![]() 在邊BC上,點N'在△ABC內.連接BN',并延長交AC于點N,NM⊥BC于點M,NP⊥MN交AB于點P,PQ⊥BC于點Q.
在邊BC上,點N'在△ABC內.連接BN',并延長交AC于點N,NM⊥BC于點M,NP⊥MN交AB于點P,PQ⊥BC于點Q.
(1)求證:四邊形PQMN為正方形;
(2)若∠A=90°,AC=1.5m,△ABC的面積=1.5m2.求PN的長.
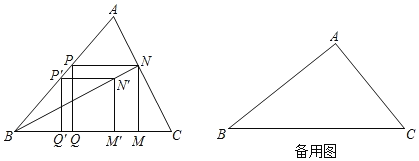
查看答案和解析>>
科目:初中數學 來源: 題型:
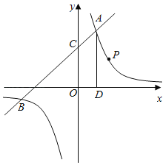
【題目】如圖,一次函數![]() 與反比例函數
與反比例函數![]() 的圖象交于點
的圖象交于點![]() 和
和![]() ,與
,與![]() 軸交于點
軸交于點![]() .
.
(1)![]() ,
,![]() ;
;
(2)根據函數圖象知,
①當![]() 時,
時,![]() 的取值范圍是 ;
的取值范圍是 ;
②當![]() 為 時,
為 時,![]() .
.
(3)過點![]() 作
作![]() 軸于點
軸于點![]() ,點
,點![]() 是反比例函數在第一象限的圖象上一點,設直線
是反比例函數在第一象限的圖象上一點,設直線![]() 與線段
與線段![]() 交于點
交于點![]() ,當
,當![]() 時,求點
時,求點![]() 的坐標.
的坐標.
(4)點![]() 是
是![]() 軸上的一個動點,當△MBC為直角三角形時,直接寫出點
軸上的一個動點,當△MBC為直角三角形時,直接寫出點![]() 的坐標.
的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
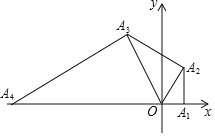
【題目】如圖,在平面直角坐標系中,點A1的坐標為(1,0),以OA1為直角邊作Rt△OA1A2,并使∠A1OA2=60°,再以OA2為直角邊作Rt△OA2A3,并使∠A2OA3=60°,再以OA3為直角邊作Rt△OA3A4,并使∠A3OA4=60°…按此規律進行下去,則點A2020的坐標為____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了幫助本市一名患“白血病”的高中生,某班15名同學積極捐款,他們捐款數額如下表:
捐款的數額(單位:元) | 5 | 10 | 20 | 50 | 100 |
人數(單位:個) | 2 | 4 | 5 | 3 | 1 |
關于這15名同學所捐款的數額,下列說法正確的是
A.眾數是100 B.平均數是30 C.極差是20 D.中位數是20
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】鄂爾多斯市某百貨商場銷售某一熱銷商品A,其進貨和銷售情況如下:用16000元購進一批該熱銷商品A,上市后很快銷售一空,根據市場需求情況,該商場又用7500元購進第二批該商品,已知第二批所購件數是第一批所購件數的一半,且每件商品的進價比第一批的進價少10元.
(1)求商場第二批商品A的進價;
(2)商場同時銷售另一種熱銷商品B,已知商品B的進價與第二批商品A的進價相同,且最初銷售價為165元,每天能賣出125件,經市場銷售發現,若售價每上漲1元,其每天銷售量就減少5件,問商場該如何定售價,每天才能獲得最大利潤?并求出每天的最大利潤是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
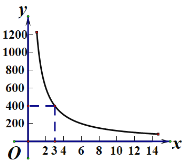
【題目】小明同學訓練某種運算技能,每次訓練完成相同數量的題目,各次訓練題目難度相當.當訓練次數不超過15次時,完成一次訓練所需要的時間y(單位:秒)與訓練次數x(單位:次)之間滿足如圖所示的反比例函數關系.完成第3次訓練所需時間為400秒.
(1)求y與x之間的函數關系式;
(2)當x的值為6,8,10時,對應的函數值分別為y1,y2,y3,比較(y1-y2)與(y2-y3)的大小: y1-y2 y2-y3.
查看答案和解析>>
科目:初中數學 來源: 題型:
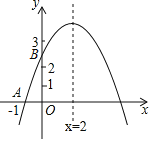
【題目】如圖,二次函數y=ax2+bx+c的圖象與x軸交于點A(﹣1,0),與y軸的交點B在(0,2)與(0,3)之間(不包括這兩點),對稱軸為直線x=2.下列結論:abc<0;②9a+3b+c>0;③若點M(![]() ,y1),點N(
,y1),點N(![]() ,y2)是函數圖象上的兩點,則y1<y2;④﹣
,y2)是函數圖象上的兩點,則y1<y2;④﹣![]() <a<﹣
<a<﹣![]() .其中正確結論有( )
.其中正確結論有( )
A. 1個 B. 2個 C. 3個 D. 4個
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com