
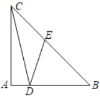
【題目】如圖,![]() 是等腰直角三角形,
是等腰直角三角形,![]() ,
,![]() ,
,![]() ,
,![]() ,那么
,那么![]() ________.
________.
【答案】![]()
【解析】
過(guò)點(diǎn)D作DF⊥BC于F,根據(jù)勾股定理即可求出BC,設(shè)![]() =x,根據(jù)等邊對(duì)等角、三角形外角的性質(zhì)和三角形的內(nèi)角和定理即可求出∠DEB,再利用銳角三角函數(shù)即可求出EF和BF,最后根據(jù)BF+EF+CE=BC列出方程即可求出結(jié)論.
=x,根據(jù)等邊對(duì)等角、三角形外角的性質(zhì)和三角形的內(nèi)角和定理即可求出∠DEB,再利用銳角三角函數(shù)即可求出EF和BF,最后根據(jù)BF+EF+CE=BC列出方程即可求出結(jié)論.
解:過(guò)點(diǎn)D作DF⊥BC于F

∵![]() 是等腰直角三角形,
是等腰直角三角形,![]() ,
,![]()
∴AB=AC=1,∠B=45°
∴BC=![]() ,△BDF為等腰直角三角形,DF=BF
,△BDF為等腰直角三角形,DF=BF
設(shè)![]() =x
=x
∴∠ECD=∠EDC
∴∠DEB=∠ECD+∠EDC=2∠EDC
∴![]() =
=![]() (180°-∠EDC)=90°-
(180°-∠EDC)=90°-![]() ∠EDC
∠EDC
∵∠DEB+∠EDB+∠B=180°
∴2∠EDC+90°-![]() ∠EDC+45°=180°
∠EDC+45°=180°
解得:∠EDC=30°
∴∠DEB=60°
∴EF=DE·cos∠DEF=![]() x,DF=DE·sin∠DEF=
x,DF=DE·sin∠DEF=![]() x
x
∴BF=DF=![]() x
x
∵BF+EF+CE=BC
∴![]() x+
x+![]() x+x=
x+x=![]()
解得:x=![]()
即CE=![]()
故答案為:![]() .
.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】某公司計(jì)劃投資![]() 萬(wàn)元引進(jìn)一條汽車配件流水生產(chǎn)線,經(jīng)過(guò)調(diào)研知道該流水生產(chǎn)線的年產(chǎn)量為
萬(wàn)元引進(jìn)一條汽車配件流水生產(chǎn)線,經(jīng)過(guò)調(diào)研知道該流水生產(chǎn)線的年產(chǎn)量為![]() 件,每件總成本為
件,每件總成本為![]() 萬(wàn)元,每件出廠價(jià)
萬(wàn)元,每件出廠價(jià)![]() 萬(wàn)元;流水生產(chǎn)線投產(chǎn)后,從第
萬(wàn)元;流水生產(chǎn)線投產(chǎn)后,從第![]() 年到第
年到第![]() 年的維修、保養(yǎng)費(fèi)用累計(jì)
年的維修、保養(yǎng)費(fèi)用累計(jì)![]() (萬(wàn)元)如下表:
(萬(wàn)元)如下表:
第 |
|
|
|
|
|
| ··· |
維修、保養(yǎng)費(fèi)用累計(jì) |
|
|
|
|
|
| ··· |
若上表中第![]() 年的維修、保養(yǎng)費(fèi)用累計(jì)
年的維修、保養(yǎng)費(fèi)用累計(jì)![]() (萬(wàn)元)與
(萬(wàn)元)與![]() 的數(shù)量關(guān)系符合我們已經(jīng)學(xué)過(guò)的一次函數(shù)、二次函數(shù)、反比例函數(shù)中某一個(gè).
的數(shù)量關(guān)系符合我們已經(jīng)學(xué)過(guò)的一次函數(shù)、二次函數(shù)、反比例函數(shù)中某一個(gè).
(1)求出![]() 關(guān)于
關(guān)于![]() 的函數(shù)解析式;
的函數(shù)解析式;
(2)投產(chǎn)第幾年該公司可收回![]() 萬(wàn)元的投資?
萬(wàn)元的投資?
(3)投產(chǎn)多少年后,該流水線要報(bào)廢(規(guī)定當(dāng)年的盈利不大于維修、保養(yǎng)費(fèi)用累計(jì)即報(bào)費(fèi))?
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知拋物線y=a(x﹣m)2+2m(m≠0)經(jīng)過(guò)原點(diǎn),其頂點(diǎn)為P,與x軸的另一交點(diǎn)為A.
(1)P點(diǎn)坐標(biāo)為 ,A點(diǎn)坐標(biāo)為 ;(用含m的代數(shù)式表示)
(2)求出a,m之間的關(guān)系式;
(3)當(dāng)m>0時(shí),若拋物線y=a(x﹣m)2+2m向下平移m個(gè)單位長(zhǎng)度后經(jīng)過(guò)點(diǎn)(1,1),求此拋物線的表達(dá)式;
(4)若拋物線y=a(x﹣m)2+2m向下平移|m|個(gè)單位長(zhǎng)度后與x軸所截的線段長(zhǎng),與平移前相比有什么變化?請(qǐng)直接寫出結(jié)果.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】拋物線y=ax2+bx+c(a≠0)的對(duì)稱軸為直線x=1,與x軸的一個(gè)交點(diǎn)坐標(biāo)為(-1,0),其部分圖象如圖所示,下列結(jié)論:① 4ac<b2;② 方程ax2+bx+c=0的兩個(gè)根分別是x1=-1,x2=3;③ 3a+c>0;④當(dāng) y>0時(shí),x的取值范圍是-1<x<3;⑤ 當(dāng)x<0時(shí),y隨x的增大而增大.其中正確的結(jié)論序號(hào)有_____________________.

查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】學(xué)以致用:?jiǎn)栴}1:怎樣用長(zhǎng)為![]() 的鐵絲圍成一個(gè)面積最大的矩形?
的鐵絲圍成一個(gè)面積最大的矩形?
小學(xué)時(shí)我們就知道結(jié)論:圍成正方形時(shí)面積最大,即圍成邊長(zhǎng)為![]() 的正方形時(shí)面積最大為
的正方形時(shí)面積最大為![]() .請(qǐng)用你所學(xué)的二次函數(shù)的知識(shí)解釋原因.
.請(qǐng)用你所學(xué)的二次函數(shù)的知識(shí)解釋原因.
思考驗(yàn)證:?jiǎn)栴}2:怎樣用鐵絲圍一個(gè)面積為![]() 且周長(zhǎng)最小的矩形?
且周長(zhǎng)最小的矩形?
小明猜測(cè):圍成正方形時(shí)周長(zhǎng)最小.
為了說(shuō)明其中的道理,小明翻閱書籍,找到下面的結(jié)論:
在![]() 、
、![]() 均為正實(shí)數(shù))中,若
均為正實(shí)數(shù))中,若![]() 為定值
為定值![]() ,則
,則![]() ,只有當(dāng)
,只有當(dāng)![]() 時(shí),
時(shí),![]() 有最小值
有最小值![]() .
.
思考驗(yàn)證:證明:![]() 、
、![]() 均為正實(shí)數(shù))
均為正實(shí)數(shù))
請(qǐng)完成小明的證明過(guò)程:
證明:對(duì)于任意正實(shí)數(shù)![]() 、
、![]()
![]()
![]()
![]()
解決問(wèn)題:
(1)若![]() ,則
,則![]() (當(dāng)且僅當(dāng)
(當(dāng)且僅當(dāng)![]() 時(shí)取“
時(shí)取“![]() ”
” ![]() ;
;
(2)運(yùn)用上述結(jié)論證明小明對(duì)問(wèn)題2的猜測(cè);
(3)填空:當(dāng)![]() 時(shí),
時(shí),![]() 的最小值為 .
的最小值為 .
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在平面直角坐標(biāo)系中,![]() 為坐標(biāo)原點(diǎn),點(diǎn)
為坐標(biāo)原點(diǎn),點(diǎn)![]() ,點(diǎn)
,點(diǎn)![]() ,點(diǎn)
,點(diǎn)![]() 為
為![]() 中點(diǎn),點(diǎn)
中點(diǎn),點(diǎn)![]() 與點(diǎn)
與點(diǎn)![]() 關(guān)于
關(guān)于![]() 軸對(duì)稱.
軸對(duì)稱.

(1)點(diǎn)![]() 的坐標(biāo)為___________;
的坐標(biāo)為___________;
(2)連結(jié)![]() ,求
,求![]() 的正切值;
的正切值;
(3)拋物線![]() 的對(duì)稱軸為直線
的對(duì)稱軸為直線![]() ,在拋物線上是否存在點(diǎn)
,在拋物線上是否存在點(diǎn)![]() (
(![]() 、
、![]() 不重合),使
不重合),使![]() 與
與![]() 全等?若存在,求出點(diǎn)
全等?若存在,求出點(diǎn)![]() 的坐標(biāo);若不存在,請(qǐng)說(shuō)明理由.
的坐標(biāo);若不存在,請(qǐng)說(shuō)明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
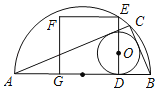
【題目】如圖,AB為半圓的直徑,C是半圓弧上一點(diǎn),正方形DEFG的一邊DG在直徑AB上,另一邊DE過(guò)△ABC的內(nèi)切圓圓心O,且點(diǎn)E在半圓上.
(1)當(dāng)正方形的頂點(diǎn)F也在半圓弧上時(shí),半圓的半徑與正方形邊長(zhǎng)的比為 ;
(2)當(dāng)正方形DEFG的面積為100,且△ABC的內(nèi)切圓⊙O的半徑r=4,求半圓的直徑AB的值;
(3)若半圓的半徑為R,直接寫出⊙O半徑r可取得的最大值.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
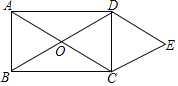
【題目】如圖,矩形ABCD對(duì)角線AC、BD交于點(diǎn)O,邊AB=6,AD=8,四邊形OCED為菱形,若將菱形OCED繞點(diǎn)O旋轉(zhuǎn)一周,旋轉(zhuǎn)過(guò)程中OE與矩形ABCD的邊的交點(diǎn)始終為M,則線段ME的長(zhǎng)度可取的整數(shù)值為___________________.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
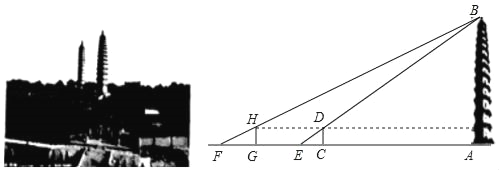
【題目】太原雙塔寺又名永祚寺,是國(guó)家級(jí)文物保護(hù)單位,由于雙塔(舍利塔、文峰塔)聳立,被人們稱為“文筆雙塔”,是太原的標(biāo)志性建筑之一,某校社會(huì)實(shí)踐小組為了測(cè)量舍利塔的高度,在地面上的C處垂直于地面豎立了高度為2米的標(biāo)桿CD,這時(shí)地面上的點(diǎn)E,標(biāo)桿的頂端點(diǎn)D,舍利塔的塔尖點(diǎn)B正好在同一直線上,測(cè)得EC=4米,將標(biāo)桿CD向后平移到點(diǎn)C處,這時(shí)地面上的點(diǎn)F,標(biāo)桿的頂端點(diǎn)H,舍利塔的塔尖點(diǎn)B正好在同一直線上(點(diǎn)F,點(diǎn)G,點(diǎn)E,點(diǎn)C與塔底處的點(diǎn)A在同一直線上),這時(shí)測(cè)得FG=6米,GC=53米.
請(qǐng)你根據(jù)以上數(shù)據(jù),計(jì)算舍利塔的高度AB.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com