
【題目】已知:如圖1,在平面直角坐標系中,拋物線![]() 與
與![]() 軸交于點
軸交于點![]() 、
、![]() (
(![]() 左
左![]() 右),與
右),與![]() 軸交于點
軸交于點![]() ,且
,且![]() .
.
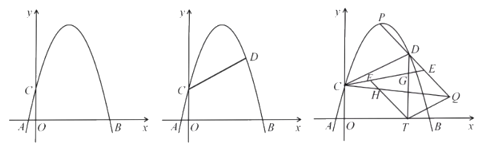
(1)求拋物線的解析式;
(2)如圖2,點![]() 在第一象限拋物線上,連接
在第一象限拋物線上,連接![]() ,若
,若![]() ,求點
,求點![]() 的坐標;
的坐標;
(3)在(2)的條件下,如圖3,過點![]() 作
作![]() 軸,線段
軸,線段![]() 經過點
經過點![]() ,與拋物線交于點
,與拋物線交于點![]() ,連接
,連接![]() 、
、![]() ,
,![]() ,點
,點![]() 在線段
在線段![]() 上,連接
上,連接![]() ,交
,交![]() 于點
于點![]() ,點
,點![]() 在
在![]() 上,連接
上,連接![]() ,交
,交![]() 于點
于點![]() ,若
,若![]() ,
,![]() ,
,![]() ,求點
,求點![]() 的坐標.
的坐標.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)根據拋物線解析式求出C點坐標,由![]() 求出B點坐標,代入原解析式即可求得參數值,即可求得拋物線解析式;
求出B點坐標,代入原解析式即可求得參數值,即可求得拋物線解析式;
(2)過點![]() 作
作![]() 軸,垂足為
軸,垂足為![]() ,利用三角函數值求得
,利用三角函數值求得![]() ,設
,設![]() ,根據點D與點K縱坐標相等結合
,根據點D與點K縱坐標相等結合![]() ,列等式求m的值,即可求解點D坐標;
,列等式求m的值,即可求解點D坐標;
(3)連接![]() 、
、![]() 、
、![]() ,延長
,延長![]() 交
交![]() 于點
于點![]() ,過
,過![]() 作
作![]() 軸,垂足為
軸,垂足為![]() ,由(2)中已知可求
,由(2)中已知可求![]() 為等邊三角形;由
為等邊三角形;由![]() ∥
∥![]() ,
,![]() ,易證
,易證![]() 為等邊三角形;結合兩個等邊三角形,可證
為等邊三角形;結合兩個等邊三角形,可證![]() ≌
≌![]() ,可得
,可得![]() ,又已知
,又已知![]() ,易證
,易證![]() ≌
≌![]() ,則
,則![]() ,可得
,可得![]() 為等邊角形,則可推導
為等邊角形,則可推導![]() ,得
,得![]() ∥
∥![]() ,結合已知
,結合已知![]() ∥
∥![]() ,證明四邊形
,證明四邊形![]() 為平行四邊形;由平行線分線段成比例,且
為平行四邊形;由平行線分線段成比例,且![]() ,可求
,可求![]() ;解Rt△QNT,可求
;解Rt△QNT,可求![]() ,再根據D、Q兩點利用待定系數法求直線
,再根據D、Q兩點利用待定系數法求直線![]() 的解析式,聯立直線DQ與拋物線解析式,即可求得交點P的坐標.
的解析式,聯立直線DQ與拋物線解析式,即可求得交點P的坐標.
解:(1)令![]() ,
,![]() ,
,
∴![]() ,即
,即![]()
∵![]() ,
,
∴![]() ,即
,即![]()
將點B代入解析式得:![]() ,
,
∴![]()
∴拋物線解析式為:![]()
(2)過點![]() 作
作![]() 軸,垂足為
軸,垂足為![]() ,
,
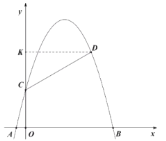
∵![]() ,
,
∴![]() ,
,
在![]() 中,
中,![]() ,
,
即![]() ,
,![]() ,
,
設![]() ,
,
∴![]() ,
,
解得:![]() (舍去),
(舍去),![]() ,
,
∴![]() ;
;
(3)連接![]() 、
、![]() 、
、![]() ,延長
,延長![]() 交
交![]() 于點
于點![]() ,過
,過![]() 作
作![]() 軸,垂足為
軸,垂足為![]() ,
,

由(2)中![]() ,
,
∴![]() ,
,
∵![]() 軸,(2)中求得
軸,(2)中求得![]() ,
,
∴![]() ,
,![]()
∴![]() 為等邊三角形
為等邊三角形
∵![]() ∥
∥![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() 為等邊三角形,
為等邊三角形,
∵![]() ,
,![]() ,
,![]() ,
,
∴![]() ≌
≌![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ≌
≌![]() ,
,
∴![]() ,
,![]() ,
,![]()
∴![]() ,
,
∴![]() 為等邊角形,
為等邊角形,
∴![]()
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ∥
∥![]() ,
,
∴四邊形![]() 為平行四邊形,
為平行四邊形,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
設直線![]() 的解析式為
的解析式為![]() ,
,
∴ ,解得
,解得 ,
,
∴![]() ,
,
設![]() ,
,
∴![]() ,
,
解得:![]() (舍去),
(舍去),![]()
∴![]() .
.


科目:初中數學 來源: 題型:
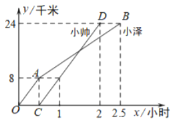
【題目】小澤和小帥兩同學分別從甲地出發,騎自行車沿同一條路到乙地參加社會實踐活動.如圖折線![]() 和線段
和線段![]() 分別表示小澤和小帥離甲地的距離
分別表示小澤和小帥離甲地的距離![]() (單位:千米)與時間
(單位:千米)與時間![]() (單位:小時)之間函數關系的圖象,則當小帥到達乙地時,小澤距乙地的距離為_________千米.
(單位:小時)之間函數關系的圖象,則當小帥到達乙地時,小澤距乙地的距離為_________千米.
查看答案和解析>>
科目:初中數學 來源: 題型:
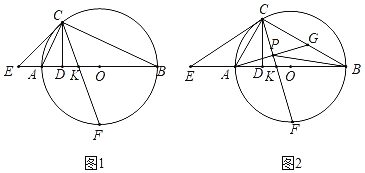
【題目】如圖1,AB是⊙O的直徑,C是⊙O上一點,CD⊥AB于D,E是BA廷長線上一點,連接CE,∠ACE=∠ACD,K是線段AO上一點,連接CK并延長交⊙O于點F.
(1)求證:CE是⊙O的切線;
(2)若AD=DK,求證:AKAO=KBAE;
(3)如圖2,若AE=AK,![]() ,點G是BC的中點,AG與CF交于點P,連接BP.請猜想PA,PB,PF的數量關系,并證明.
,點G是BC的中點,AG與CF交于點P,連接BP.請猜想PA,PB,PF的數量關系,并證明.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】中華文明,源遠流長;中華漢字,寓意深廣.為了傳承優秀傳統文化,某校團委組織了一次全校1000名學生參加的“漢字聽寫”大賽,賽后發現所有參賽學生的成績均不低于50分.為了更好地了解本次大賽的成績分布情況,隨機抽取了200名學生的成績(成績![]() 取整數,總分100分)作為樣本進行整理,得到下列不完整的統計圖表:
取整數,總分100分)作為樣本進行整理,得到下列不完整的統計圖表:
成績 | 頻數 | 頻率 |
| 10 | 0.05 |
| 20 | 0.10 |
| 30 |
|
|
| 0.30 |
| 80 | 0.40 |
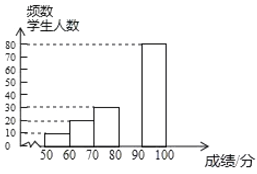
請根據所給的信息,解答下列問題:
(1)![]() _____,
_____,![]() _____;
_____;
(2)請補全頻數分布直方圖;
(3)這次比賽成績的中位數會落在______分數段;
(4)若成績在90分以上(包括90分)的為優等,則該校參加這次比賽的1000名學生中成績優等的大約有多少人?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,大海中某燈塔P周圍10海里范圍內有暗礁,一艘海輪在點A處觀察燈塔P在北偏東60°方向,該海輪向正東方向航行8海里到達點B處,這時觀察燈塔P恰好在北偏東45°方向.如果海輪繼續向正東方向航行,會有觸礁的危險嗎?試說明理由.(參考數據:![]() ≈1.73)
≈1.73)
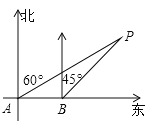
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,矩形EFGH的頂點E,G分別在菱形ABCD的邊AD ,BC上,頂點F,H在菱形ABCD的對角線BD上,若AB=6,∠A=120°,且DE=2,則FH=_______.
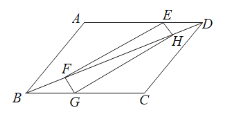
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,頂點為![]() 的拋物線
的拋物線![]() 與
與![]() 軸的另一個交點為
軸的另一個交點為![]() ,連接
,連接![]() .
.
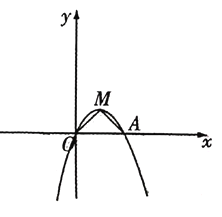
(1)求拋物線![]() 的函數表達式;
的函數表達式;
(2)已知點![]() 的坐標為
的坐標為![]() ,將拋物線
,將拋物線![]() 向上平移得到拋物線
向上平移得到拋物線![]() ,拋物線
,拋物線![]() 與
與![]() 軸分別交于點
軸分別交于點![]() (點
(點![]() 在點
在點![]() 的左側),如果
的左側),如果![]() 與
與![]() 相似,求所有符合條件的拋物線
相似,求所有符合條件的拋物線![]() 的函數表達式.
的函數表達式.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小夏同學從家到學校有![]() ,
,![]() 兩條不同的公交線路.為了解早高峰期間這三條線路上的公交車從甲地到乙地的用時情況,在每條線路上隨機選取了500個班次的公交車,收集了這些班次的公交車用時(單位:分鐘)的數據,統計如下:
兩條不同的公交線路.為了解早高峰期間這三條線路上的公交車從甲地到乙地的用時情況,在每條線路上隨機選取了500個班次的公交車,收集了這些班次的公交車用時(單位:分鐘)的數據,統計如下:
公交車用時 頻數 公交車路線 |
|
|
|
| 總計 |
| 59 | 151 | 166 | 124 | 500 |
| 43 | 57 | 149 | 251 | 500 |
據此估計,早高峰期間,乘坐![]() 線路“用時不超過35分鐘”的概率為__________,若要在40分鐘之內到達學校,應盡量選擇乘坐__________(填
線路“用時不超過35分鐘”的概率為__________,若要在40分鐘之內到達學校,應盡量選擇乘坐__________(填![]() 或
或![]() )線路.
)線路.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com