
【題目】⊙![]() 的兩條弦
的兩條弦![]() ,
, ![]() 相交于點
相交于點![]() .
.
(![]() )若
)若![]() ,且
,且![]() ,
, ![]() ,求
,求![]() 的長.
的長.
(![]() )若
)若![]() 是⊙
是⊙![]() 的直徑,
的直徑, ![]() ,且
,且![]() ,
, ![]() ,求⊙
,求⊙![]() 的半徑.
的半徑.
 口算能手系列答案
口算能手系列答案科目:初中數學 來源: 題型:
【題目】如圖,在以O為原點的直角坐標系中,矩形OABC的兩邊OC、OA分別在x軸、y軸的正半軸上,反比例函數y=![]() (x>0)的圖象與AB相交于點D,與BC相交于點E,若BD=3AD,且△ODE的面積為30,則k的值是_____.
(x>0)的圖象與AB相交于點D,與BC相交于點E,若BD=3AD,且△ODE的面積為30,則k的值是_____.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀材料,解決問題
材料一:《孟子》中記載有一尺之棰,日取其半,萬世不竭,其中蘊含了“有限”與“無限”的關系.如果我們要計算到第n天時,累積取走了多長的木棒?可以用下面兩種方法去解決:
方法一:第n天,留下了![]() 尺木棒,那么累積取走了
尺木棒,那么累積取走了![]() 尺木棒.
尺木棒.
方法二:第1天取走了![]() 尺木棒,第2天取走了
尺木棒,第2天取走了![]() 尺木棒,……第n天取走了
尺木棒,……第n天取走了![]() 尺木棒,那么累積取走了:
尺木棒,那么累積取走了:![]() 尺木棒.
尺木棒.
設:![]() ……①
……①
由①×![]() 得:
得:![]() ……②
……②
①-②得:![]() 則:
則:![]()
材料二:關于數學家高斯的故事,200多年前,高斯的算術老師提出了下面的問題:1+2+3+…+100=?據說當其他同學忙于把100個數逐項相加時,十歲的高斯卻用下面的方法迅速算出了正確的答案:(1+100)+(2+99)+…+(50+51)=101×50=5050.
也可以這樣理解:令S=1+2+3+4+…+100 ①,則S=100+99+98+…+3+2+1②
①+②得:2S=(1+100)+(2+99)+(3+98)+…+(100+1)=100×(1+100)
即![]()
請用你學到的方法解決以下問題:
(1)計算:![]() ;
;
(2)我國古代數學名著《算法統宗》中有如下問題:“遠望巍巍塔七層,紅光點點倍加增,共燈三百八十一,請問尖頭幾盞燈?”意思是:一座7層塔共掛了381盞燈,且相鄰兩層中的下一層燈數是上一層的2倍,問塔的頂層共有多少盞燈?
(3)某中學“數學社團”開發了一款應用軟件,推出了“解數學題獲取軟件激活碼”的活動,某一周,這款軟件的激活碼為下面數學問題的答案:已知一列數1,1,2,1,2,4,1,2,4,8,1,2,4,8,16,……其中第1項是![]() ,接下來的兩項是
,接下來的兩項是![]() ,
,![]() ,再接下來的三項是
,再接下來的三項是![]() ,
,![]() ,
,![]() ,以此類推,求滿足如下條件的正整數N:
,以此類推,求滿足如下條件的正整數N:![]() ,且這一列數前N項和為2的正整數冪,請求出所有滿足條件的軟件激活碼正整數N的值.
,且這一列數前N項和為2的正整數冪,請求出所有滿足條件的軟件激活碼正整數N的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,把一個木制正方體的表面涂上顏色,然后將正方形分割成27個大小相同的小正方體,從這些小正方體中任意取出一個,求取出的小正方體;
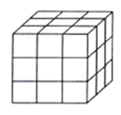
(1)只有一面涂有顏色的概率;
(2)至少有兩面涂有顏色的概率;
(3)各個面都沒有顏色的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知,△ABC為等邊三角形,點D為AC上的一個動點,點E為BC延長線上一點,且BD=DE.
(1)如圖1,若點D在邊AC上,猜想線段AD與CE之間的關系,并說明理由;
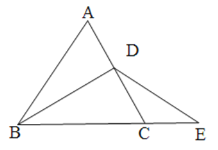
圖1
(2)如圖2,若點D在AC的延長線上,(1)中的結論是否成立,請說明理由.
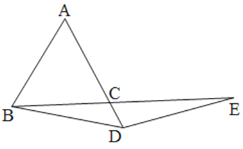
圖2
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我市某中學舉行“中國夢——校園好聲音”歌手大賽,高、初中部根據初賽成績,各選出5名選手組成初中代表隊和高中代表隊參加學校決賽.兩個隊各選出的5名選手的決賽成績如圖所示.

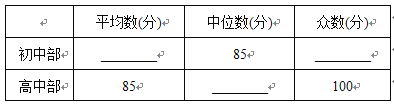
(1)根據圖示填寫下表;
(2)結合兩隊成績的平均數和中位數,分析哪個隊的決賽成績較好;
(3)計算兩隊決賽成績的方差并判斷哪一個代表隊選手成績較為穩定.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知![]() ,
,![]() ,求
,求![]() 的度數.
的度數.

(1)填空,在空白處填上結果或者理由.
解:過點![]() 作
作![]() ,(如圖)
,(如圖)
得![]() ___________°, ( )
___________°, ( )
又因為![]() ,(已知)
,(已知)
所以![]() ___________°.
___________°.
因為![]() ,
,
所以![]() , ( )
, ( )
又因為![]() ,(已知)
,(已知)
所以![]() ___________°,
___________°,
所以![]() ___________°.
___________°.
(2)請用另一種解法求![]() 的度數.
的度數.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com