
【題目】某公司經銷的一種產品每件成本為40元,要求在90天內完成銷售任務.已知該產品90天內每天的銷售價格與時間(第x天)的關系如下表:
時間(第x天) | 1≤x<50 | 50≤x≤90 |
x+50 | 90 |
任務完成后,統計發現銷售員小王90天內日銷售量p(件)與時間(第x天)滿足一次函數關系p=﹣2x+200.設小王第x天銷售利潤為W元.
(1)直接寫出W與x之間的函數關系式,井注明自變量x的取值范圍;
(2)求小生第幾天的銷售量最大?最大利潤是多少?
(3)任務完成后,統計發現平均每個銷售員每天銷售利潤為4800公司制定如下獎勵制度:如果一個銷售員某天的銷售利潤超過該平均值,則該銷售員當天可獲得200元獎金.請計算小王一共可獲得多少元獎金?
【答案】(1)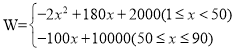 ;(2)小王第45天的銷售利潤最大,最大利潤為6050元;(3)小王一共可獲得6200元獎金.
;(2)小王第45天的銷售利潤最大,最大利潤為6050元;(3)小王一共可獲得6200元獎金.
【解析】
(1)依據題意銷售利潤=銷售量×(售價-進價)易得出銷售利潤為W(元)與x(天)之間的函數關系式;
(2)依據(1)中函數的增減性求得最大利潤;
(3)根據銷售利潤為W(元)與x(天)之間的函數關系式,求出利潤超過4800元的天數即可求得可獲得的獎金金額.
(1)依題意:![]() ,
,
整理得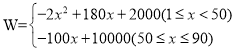 ;
;
(2)①當1≤x<50時,W=﹣2x2+180x+2000=﹣2(x﹣45)2+6050,
∵﹣2<0,
∴拋物線開口向下,
∴當x=45時,W有最大值為6050;
②當50≤x≤90時,W=﹣100x+10000,
∵﹣100<0,
∴W隨x的增大而減小,
∴當x=50時,W有最大值為5000,
∵6050>5000,
∴當x=45時,W的值最大,最大值為6050,
即小王第45天的銷售利潤最大,最大利潤為6050元;
(3)①當1≤x<50時,令W=4800,得W=﹣2(x﹣45)2+6050=4800,
解得x1=20,x2=70,
∴當W>4800時,20<x<70,
∵1≤x<50,
∴20<x<50;
②當50≤x≤90時,令W>4800,W=﹣100x+10000>4800,
解得x<52,
∵50≤x≤90,
∴50≤x<52,
綜上所述:當20<x<50時,W>4800,即共有51﹣21+1=31天的銷售利潤超過4800元,
∴可獲得獎金200×31=6200元,
即小王一共可獲得6200元獎金.


科目:初中數學 來源: 題型:
【題目】二次函數y=ax2+bx+c(a≠0)的圖象如圖,給出下列四個結論:①4ac﹣b2<0;②4a+c<2b;③3b+2c<0;④m(am+b)+b<a(m≠﹣1),其中正確結論的個數是( )
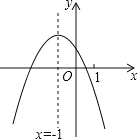
A.4個B.3個C.2個D.1個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了估計某地區供暖期間空氣質量情況,某同學在20天里做了如下記錄:
污染指數(ω) | 40 | 60 | 80 | 100 | 120 | 140 |
天數(天) | 3 | 2 | 3 | 4 | 5 | 3 |
其中ω<50時空氣質量為優,50≤ω≤100時空氣質量為良,100<ω≤150時空氣質量為輕度污染.若按供暖期125天計算,請你估計該地區在供暖期間空氣質量達到良以上(含良)的天數為( )
A.75B.65C.85D.100
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,![]() 是正方形
是正方形![]() 外一點,連接
外一點,連接![]() 交
交 ![]() 于點
于點![]() ,若
,若![]() .下列結論:①
.下列結論:①![]() ;②
;②![]() ;③ 四邊形
;③ 四邊形![]() 的面積是
的面積是![]() ;④點
;④點![]() 到 直線
到 直線![]() 的距離為
的距離為![]() ;⑤
;⑤![]() .其中結論正確的個數是( )
.其中結論正確的個數是( )
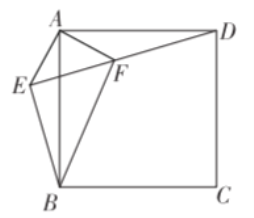
A.![]() B.2C.3D.4
B.2C.3D.4
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在國家政策的宏觀調控下,某市的商品房成交均價由今年3月份的14 000元/m2下降到5月份的12 600元/m2.
(1)問4,5兩月平均每月降價的百分率約是多少?(參考數據:![]() ≈0.95)
≈0.95)
(2)如果房價繼續跌落,按此降價的百分率,你預測到7月份該市的商品房成交均價是否會跌跛10 000元/m2?請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知一個口袋中裝有六個完全相同的小球,小球上分別標有1,2,5,7,8,13六個數,攪勻后一次從中摸出一個小球,將小球上的數記為m,則使得一次函數y=(﹣m+1)x+11﹣m經過一、二、四象限且關于x的分式方程![]() =3x+
=3x+![]() 的解為整數的概率是( )
的解為整數的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
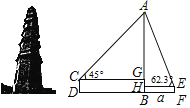
【題目】慈氏塔位于岳陽市城西洞庭湖邊,是湖南省保存最好的古塔建筑之一.如圖,小亮的目高CD為1.7米,他站在D處測得塔頂的仰角∠ACG為45°,小琴的目高EF為1.5米,她站在距離塔底中心B點a米遠的F處,測得塔頂的仰角∠AEH為62.3°.(點D、B、F在同一水平線上,參考數據:sin62.3°≈0.89,cos62.3°≈0.46,tan62.3°≈1.9)
(1)求小亮與塔底中心的距離BD;(用含a的式子表示)
(2)若小亮與小琴相距52米,求慈氏塔的高度AB.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com