
【題目】如圖1,二次函數![]() 的圖像與
的圖像與![]() 軸交于
軸交于![]() 兩點,與
兩點,與![]() 軸交于點
軸交于點![]() .
.
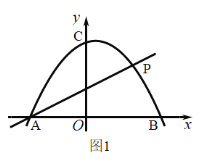
(1)求拋物線的函數關系式;
(2)點![]() 是拋物線第象限上一點,設點
是拋物線第象限上一點,設點![]() 的橫坐標為
的橫坐標為![]() ,連接
,連接![]() ,如果點
,如果點![]() 關于直線
關于直線![]() 的對稱點
的對稱點![]() 落在
落在![]() 軸下方(含
軸下方(含![]() 軸),求
軸),求![]() 的取值范圍;
的取值范圍;
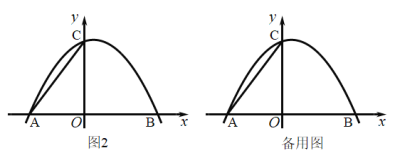
(3)如圖2,連接![]() 將
將![]() 繞平面內某點
繞平面內某點![]() 順時針旋轉
順時針旋轉![]() ,得到
,得到![]() 點
點![]() 的對應點分別是點
的對應點分別是點![]() 、若
、若![]() 的兩個項點恰好落在拋物線上,請直接寫出點
的兩個項點恰好落在拋物線上,請直接寫出點![]() 的坐標 .
的坐標 .
【答案】(1)![]() ;(2)
;(2)![]() 的取值范圍為
的取值范圍為![]() ; (3)點
; (3)點![]() 的坐標為
的坐標為![]() 或
或![]()
【解析】
(1)直接利用待定系數法即可求解;
(2)首先根據二次函數的解析式求出B,C的坐標,然后設點![]() 關于直線
關于直線![]() 對稱的點恰好在
對稱的點恰好在![]() 軸上時,對稱點為
軸上時,對稱點為![]() ,根據軸對稱的性質和勾股定理求出點E的坐標,進而求出直線AP的解析式,然后將直線AP的解析式與二次函數的解析式聯立,求出P點的橫坐標,然后數形結合即可得出答案;
,根據軸對稱的性質和勾股定理求出點E的坐標,進而求出直線AP的解析式,然后將直線AP的解析式與二次函數的解析式聯立,求出P點的橫坐標,然后數形結合即可得出答案;
(3)分兩種情況:當![]() 在二次函數圖像上時和當
在二次函數圖像上時和當![]() 在二次函數圖像上時,設點
在二次函數圖像上時,設點![]() 的坐標為
的坐標為![]() 將點的坐標代入二次函數中,通過聯立求方程組的解即可得出答案.
將點的坐標代入二次函數中,通過聯立求方程組的解即可得出答案.
![]() 二次函數
二次函數![]() 的圖象過點
的圖象過點![]()
![]()
![]()
即![]() ;
;
![]() 令
令![]() ,則
,則![]()
解得![]() ,
,
![]() ,
,
令![]() ,則
,則![]()
![]() ,
,
則![]()
設點![]() 關于直線
關于直線![]() 對稱的點恰好在
對稱的點恰好在![]() 軸上時,對稱點為
軸上時,對稱點為![]() ,
,
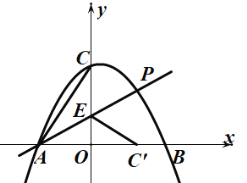
![]() ,
,
![]()
設![]() 長為
長為![]()
則![]()
在![]() 中,
中,![]() ,
,
即![]()
解得![]()
![]() 點
點![]() 的坐標為
的坐標為![]() ,
,
設直線![]() 的函數表達式為
的函數表達式為![]()
所以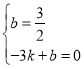 解得
解得![]()
即![]() .
.
設直線![]() 與二次函數的圖像交點的橫坐標為
與二次函數的圖像交點的橫坐標為![]() ,
,
則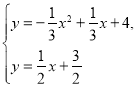
解得![]() ,
,
![]() 點
點![]() 關于直線
關于直線![]() 的對稱點
的對稱點![]() 落在
落在![]() 軸下方(含
軸下方(含![]() 軸)時,
軸)時,
![]() 的取值范圍為
的取值范圍為![]() ;
;
![]() 設點
設點![]() 的坐標為
的坐標為![]()
當![]() 在二次函數圖像上時,
在二次函數圖像上時,
則點![]() 的坐標為
的坐標為![]() 、點
、點![]() 的坐標為
的坐標為![]()
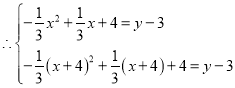
解得 ,
,
即點![]() 的坐標為
的坐標為![]() ;
;
當![]() 在二次函數圖像上時,
在二次函數圖像上時,
則點![]() 的坐標為
的坐標為![]()
 ,
,
解得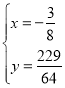
即點![]() 的坐標為
的坐標為![]()
綜上可知點![]() 的坐標為
的坐標為![]() 或
或![]()


 備戰中考寒假系列答案
備戰中考寒假系列答案科目:初中數學 來源: 題型:
【題目】2018年非洲豬瘟疫情暴發后,今年豬肉價格不斷走高,引起了民眾與政府的高度關注,據統計:今年7月20日豬肉價格比今年年初上漲了60%,某市民今年7月20日在某超市購買1千克豬肉花了80元錢.
(1)問:今年年初豬肉的價格為每千克多少元?
(2)某超市將進貨價為每千克65元的豬肉,按7月20日價格出售,平均一天能銷售出100千克,經調查表明:豬肉的售價每千克下降1元,其日銷售量就增加10千克,超市為了實現銷售豬內每天有1560元的利潤,并且可能讓顧客得到實惠,豬肉的售價應該下降多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
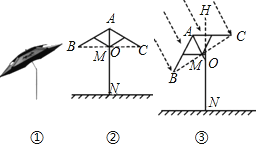
【題目】如圖①是釣魚傘,為遮擋不同方向的陽光,釣魚傘可以在撐桿AN上的點O處彎折并旋轉任意角,圖②是釣魚傘直立時的示意圖,當傘完全撐開時,傘骨AB,AC與水平方向的夾角∠ABC=∠ACB=30°,傘骨AB與AC水平方向的最大距離BC=2m,BC與AN交于點M,撐桿AN=2.2m,固定點O到地面的距離ON=1.6m.
(1)如圖②,當傘完全撐開并直立時,求點B到地面的距離.
(2)某日某時,為了增加遮擋斜射陽光的面積,將釣魚傘傾斜與鉛垂線HN成30°夾角,如圖③.
①求此時點B到地面的距離;
②若斜射陽光與BC所在直線垂直時,求BC在水平地面上投影的長度約是多少.(說明:![]() ≈1.732,結果精確到0.1m)
≈1.732,結果精確到0.1m)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】疫情初期,某市出臺《中小學教師志愿輔導工作實施意見》,鼓勵教師參與志愿輔導,該市率先示范,推出名師公益課程,為學生提供線上免費輔導,據統計,第一批公益課受益學生![]() 萬人次,第三批公益課受益人數
萬人次,第三批公益課受益人數![]() 萬人次.
萬人次.
(1)如果第二批,第三批公益課受益學生人次的增長率相同,求這個增長率;
(2)按照這個增長率,預計第四批公益課受益學生將達到多少萬人次?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某市一研究機構為了了解![]() 歲年齡段市民對創建文明城市的關注程度,隨機選取了
歲年齡段市民對創建文明城市的關注程度,隨機選取了![]() 名年齡在該范圍內的市民進行了調查,并將收集到的數據制成了尚不完整的頻數分布表、頻數分布直方圖和扇形統計圖,如下所示:
名年齡在該范圍內的市民進行了調查,并將收集到的數據制成了尚不完整的頻數分布表、頻數分布直方圖和扇形統計圖,如下所示:
組別 | 年齡段 | 頻數(人數) |
第 |
|
|
第 |
|
|
第 |
|
|
第 |
|
|
第 |
|
|
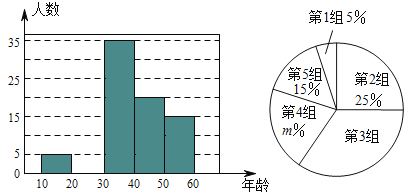
(1)請直接寫出![]() ,第
,第![]() 組人數在扇形統計圖中所對應的圓心角是 度;
組人數在扇形統計圖中所對應的圓心角是 度;
(2)請補全上面的頻數分布直方圖:
(3)假設該市現有![]() 歲的市民
歲的市民![]() 萬人,問
萬人,問![]() 歲年齡段的關注創建文明城市的人數約有多少?
歲年齡段的關注創建文明城市的人數約有多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
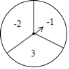
【題目】如圖,可以自由轉動的轉盤被平均分成了三等分標有數字﹣2,3,﹣1的扇形區域轉動轉盤,待轉盤自動停止后,指針指向一個扇形的內部,則該扇形內的數字即為轉出的數字,此時,稱為轉動轉盤一次(若指針指向兩個扇形的交線,則不計轉動的次數,重新轉動轉盤,直到指針指向一個扇形的內部為止)
(1)轉動轉盤一次,求轉出的數字是3的概率;
(2)轉動轉盤兩次,設第一次得到的數字為x,第二次得到的數字為y,點M的坐標為(x,y),請用樹狀圖或列表法求點M在反比例函數y=﹣![]() 的圖象上的概率.
的圖象上的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】第5代移動通信技術簡稱5G,某地已開通5G業務,經測試5G下載速度是4G下載速度的15倍,小明和小強分別用5G與4G下載一部600兆的公益片,小明比小強所用的時間快140秒,求該地4G與5G的下載速度分別是每秒多少兆?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某中學開設的體育選修課有籃球、足球、排球、羽毛球、乒乓球,學生可以根據自己的愛好選修其中1門.某班班主任對全班同學的選課情況進行了調查統計,制成了兩幅不完整的統計圖(圖(1)和圖(2)):
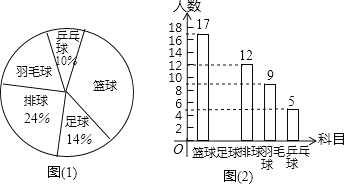
(1)請你求出該班的總人數,并補全條形圖(注:在所補小矩形上方標出人數);
(2)在該班團支部4人中,有1人選修排球,2人選修羽毛球,1人選修乒乓球.如果該班班主任要從他們4人中任選2人作為學生會候選人,那么選出的兩人中恰好有1人選修排球、1人選修羽毛球的概率是多少?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com