
【題目】下列條件中,能判定四邊形ABCD為平行四邊形的個數是( )
①AB∥CD,AD=BC ; ②AB=CD,AD=BC;③∠A=∠B,∠C=∠D; ④AB=AD,CB=CD.
A. 1個B. 2個C. 3個D. 4個
【答案】A
【解析】
根據平行四邊形的判定定理(①有兩組對邊分別平行的四邊形是平行四邊形,②有兩組對邊分別相等的四邊形是平行四邊形,③有兩組對角分別相等的四邊形是平行四邊形,④有一組對邊平行且相等的四邊形是平行四邊形,⑤對角線互相平分的四邊形是平行四邊形)進行判斷即可.
A、由AB∥CD,AD=BC,四邊形ABCD也可以是等腰梯形,故本選項錯誤;
B、∵AB=CD,AD=BC,∴四邊形ABCD是平行四邊形,故本選項正確
C、∵∠A=∠B,∠C=∠D,∠A+∠B+∠C+∠D=360°,
∴2∠B+2∠C=360°,
∴∠B+∠C=180°,
∴AB∥CD,但不能推出其它條件,即不能推出四邊形ABCD是平行四邊形,故本選項錯誤;
D、根據AB=AD,CB=CD不能推出四邊形ABCD是平行四邊形,故本選項錯誤;
故選:A.



科目:初中數學 來源: 題型:
【題目】中學生騎電動車上學給交通安全帶來隱患,為了解某中學2 500個學生家長對“中學生騎電動車上學”的態度,從中隨機調查400個家長,結果有360個家長持反對態度,則下列說法正確的是( )
A. 調查方式是普查 B. 該校只有360個家長持反對態度
C. 樣本是360個家長 D. 該校約有90%的家長持反對態度
查看答案和解析>>
科目:初中數學 來源: 題型:
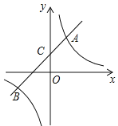
【題目】如圖,一次函數![]() 的圖像與反比例函數
的圖像與反比例函數![]() 的圖像交于點A(2,4)和點B(n,-2),與
的圖像交于點A(2,4)和點B(n,-2),與![]() 軸交于點C.
軸交于點C.
(1)求m,n的值;
(2)當![]() 時,請直接寫出
時,請直接寫出![]() 的取值范圍;
的取值范圍;
(3)點B關于![]() 軸的對稱點是B′,連接AB′,CB′,求△AB′C的面積.
軸的對稱點是B′,連接AB′,CB′,求△AB′C的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
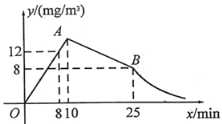
【題目】春季是流感高發的季節,為此,某校為預防流感,對教室進行熏藥消毒.在對教室進行消毒的過程中,先經過10min的藥物燃燒,再封閉教室15min,然后打開門窗進行通風.已知室內空氣中含藥量![]() 與藥物在空氣中的持續時間
與藥物在空氣中的持續時間![]() 之間的函數關系式如圖所示(即圖中線段OA、線段AB和雙曲線在點B及其右側部分),請根據圖中信息解答下列問題:
之間的函數關系式如圖所示(即圖中線段OA、線段AB和雙曲線在點B及其右側部分),請根據圖中信息解答下列問題:
(1)求藥物燃燒階段和打開門窗進行通風階段![]() 與
與![]() 之間的函數表達式;
之間的函數表達式;
(2)若室內空氣中的含藥量不低于![]() 且持續時間不少于35min,才能有效消滅病毒,則此次消毒是否有效?請說明理由.
且持續時間不少于35min,才能有效消滅病毒,則此次消毒是否有效?請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(1)2019年4月,中國新聞出版研究院發布了《第十六次全國國民閱讀調查報告》,以下是小明根據該報告提供的數據制作的“2017-2018年我國未成年人圖書閱讀率統計圖”的一部分.

報告中提到,2018年9-13周歲少年兒童圖書閱讀率比2017年提高了3.1個百分點,2017年我國0-17周歲未成年人圖書閱讀率為84.8%.
根據以上信息解決下列問題:
①寫出圖1中a的值;
②補全圖1;
(2)讀書社的小明在搜集資料的過程中,發現了《人民日報》曾經介紹過多種閱讀法,他在班上同學們介紹了其中6種,并調查了全班40名同學對這6種閱讀法的認可程度,制作了如下的統計表和統計圖:

根據以上信息解決下列問題:
①補全統計表及圖2;
②根據調查結果估計全年級500名同學最愿意使用“![]() .精華提煉法”的人數.
.精華提煉法”的人數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】探究逼近![]() 的有理近似值.
的有理近似值.
方法介紹:
經過![]() 步操作(
步操作(![]() 為正整數)不斷尋找有理數
為正整數)不斷尋找有理數![]() ,
,![]() ,使得
,使得![]() ,并且讓
,并且讓![]() 的值越來越小,同時利用數軸工具將任務幾何化,直觀理解通過等分線段的方法不斷縮小
的值越來越小,同時利用數軸工具將任務幾何化,直觀理解通過等分線段的方法不斷縮小![]() 對應的點
對應的點![]() 所在線段的長度(二分法)
所在線段的長度(二分法)
思路
在數軸上記![]() ,
,![]() 對應的點分別為
對應的點分別為![]() ,
,![]() 和
和![]() 的平均數
的平均數![]() 對應線段
對應線段![]() 的中點(記為
的中點(記為![]() ).通過判斷
).通過判斷![]() 還是
還是![]() ,得到點
,得到點![]() 是在二等分后的“左線段
是在二等分后的“左線段![]() ”上還是“右線段
”上還是“右線段![]() ”上,重復上述步驟,不斷得到
”上,重復上述步驟,不斷得到![]() ,從而得到
,從而得到![]() 更精確的近似值.
更精確的近似值.
具體操作步驟及填寫“閱讀活動任務單”:
(1)當![]() 時,
時,
①尋找左右界值:先尋找兩個連續正整數![]() ,使得
,使得![]() .
.
因為![]() ,所以
,所以![]() ,那么
,那么![]() ,
,![]() ,線段
,線段![]() 的中點
的中點![]() 對應的數
對應的數![]() .
.
②二分定位:判斷點![]() 在“左線段
在“左線段![]() ”上還是在“右線段
”上還是在“右線段![]() ”上.
”上.
比較7與![]() 的大小,從而確定
的大小,從而確定![]() 與
與![]() 的大小;
的大小;
因為![]() >
> ![]() (填 “>”或“<”),得到點
(填 “>”或“<”),得到點![]() 在線段
在線段 ![]() 上(填“
上(填“![]() ”或“
”或“![]() ”).
”).
(2)當![]() 時,在(1)中所得
時,在(1)中所得![]() 的基礎上,仿照以上步驟,繼續進行下去,得到表中
的基礎上,仿照以上步驟,繼續進行下去,得到表中![]() 時的相應內容.
時的相應內容.
請繼續仿照以上步驟操作下去,補全“閱讀活動任務單”:
|
|
|
|
| 點 | 得出更精確的 |
1 | 2 | 3 | 2.5 |
| 點 |
|
2 | 2.5 | 3 | 2.75 |
| 點 |
|
3 | 2.5 | 2.75 | 2.625 |
| ||
4 |
查看答案和解析>>
科目:初中數學 來源: 題型:
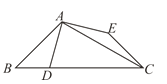
【題目】如圖,△ABC中,∠ABC=45°,∠BCA=30°,點D在BC上,點E在△ABC外,且AD=AE=CE,AD⊥AE,則![]() 的值為____________.
的值為____________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(2016四川省攀枝花市)某市為了鼓勵居民節約用水,決定實行兩級收費制度.若每月用水量不超過14噸(含14噸),則每噸按政府補貼優惠價m元收費;若每月用水量超過14噸,則超過部分每噸按市場價n元收費.小明家3月份用水20噸,交水費49元;4月份用水18噸,交水費42元.
(1)求每噸水的政府補貼優惠價和市場價分別是多少?
(2)設每月用水量為x噸,應交水費為y元,請寫出y與x之間的函數關系式;
(3)小明家5月份用水26噸,則他家應交水費多少元?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com