
【題目】在平面直角坐標系![]() 中(如圖),已知二次函數
中(如圖),已知二次函數![]() (其中a、b、c是常數,且a≠0)的圖像經過點A(0,-3)、B(1,0)、C(3,0),聯結AB、AC.
(其中a、b、c是常數,且a≠0)的圖像經過點A(0,-3)、B(1,0)、C(3,0),聯結AB、AC.
(1)求這個二次函數的解析式;
(2)點D是線段AC上的一點,聯結BD,如果![]() ,求tan∠DBC的值;
,求tan∠DBC的值;
(3)如果點E在該二次函數圖像的對稱軸上,當AC平分∠BAE時,求點E的坐標.

【答案】(1)![]() ;(2)
;(2)![]() ;(3)E(2,
;(3)E(2,![]() )
)
【解析】
(1)直接利用待定系數法,把A、B、C三點代入解析式,即可得到答案;
(2)過點D作DH⊥BC于H,在△ABC中,設AC邊上的高為h,利用面積的比得到![]() ,然后求出DH和BH,即可得到答案;
,然后求出DH和BH,即可得到答案;
(3)延長AE至x軸,與x軸交于點F,先證明△OAB∽△OFA,求出點F的坐標,然后求出直線AF的方程,即可求出點E的坐標.
解:(1)將A(0,-3)、B(1,0)、C(3,0)代入![]() 得,
得,
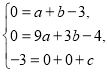
解得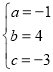 ,
,
∴此拋物線的表達式是:![]() .
.
(2)過點D作DH⊥BC于H,

在△ABC中,設AC邊上的高為h,則![]() ,
,
又∵DH//y軸,
∴![]() .
.
∵OA=OC=3,則∠ACO=45°,
∴△CDH為等腰直角三角形,
∴![]() .
.
∴![]() .
.
∴tan∠DBC=![]() .
.
(3)延長AE至x軸,與x軸交于點F,

∵OA=OC=3,
∴∠OAC=∠OCA=45°,
∵∠OAB=∠OAC![]() ∠BAC=45°
∠BAC=45°![]() ∠BAC,∠OFA=∠OCA
∠BAC,∠OFA=∠OCA![]() ∠FAC=45°
∠FAC=45°![]() ∠FAC,
∠FAC,
∵∠BAC=∠FAC,
∴∠OAB=∠OFA.
∴△OAB∽△OFA,
∴![]() .
.
∴OF=9,即F(9,0);
設直線AF的解析式為y=kx+b(k≠0),
可得![]() ,解得
,解得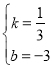 ,
,
∴直線AF的解析式為:![]() ,
,
將x=2代入直線AF的解析式得:![]() ,
,
∴E(2,![]() ).
).


 尖子生新課堂課時作業系列答案
尖子生新課堂課時作業系列答案 英才計劃同步課時高效訓練系列答案
英才計劃同步課時高效訓練系列答案科目:初中數學 來源: 題型:
【題目】把函數![]() 的圖象繞點
的圖象繞點![]() 旋轉
旋轉![]() ,得到新函數
,得到新函數![]() 的圖象,我們稱
的圖象,我們稱![]() 是
是![]() 關于點
關于點![]() 的相關函數.
的相關函數.![]() 的圖象的對稱軸與
的圖象的對稱軸與![]() 軸交點坐標為
軸交點坐標為![]() .
.
(1)填空:![]() 的值為 (用含
的值為 (用含![]() 的代數式表示)
的代數式表示)
(2)若![]() ,當
,當![]() 時,函數
時,函數![]() 的最大值為
的最大值為![]() ,最小值為
,最小值為![]() ,且
,且![]() ,求
,求![]() 的解析式;
的解析式;
(3)當![]() 時,
時,![]() 的圖象與
的圖象與![]() 軸相交于
軸相交于![]() 兩點(點
兩點(點![]() 在點
在點![]() 的右側).與
的右側).與![]() 軸相交于點
軸相交于點![]() .把線段
.把線段![]() 原點
原點![]() 逆時針旋轉
逆時針旋轉![]() ,得到它的對應線段
,得到它的對應線段![]() ,若線
,若線![]() 與
與![]() 的圖象有公共點,結合函數圖象,求
的圖象有公共點,結合函數圖象,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某工廠有甲種原料![]() ,乙種原料
,乙種原料![]() ,現用兩種原料生產處
,現用兩種原料生產處![]() 兩種產品共
兩種產品共![]() 件,已知生產每件
件,已知生產每件![]() 產品需甲種原料
產品需甲種原料![]() ,乙種原料
,乙種原料![]() ,且每件
,且每件![]() 產品可獲得
產品可獲得![]() 元;生產每件
元;生產每件![]() 產品甲種原料
產品甲種原料![]() ,乙種原料
,乙種原料![]() ,且每件
,且每件![]() 產品可獲利潤
產品可獲利潤![]() 元,設生產
元,設生產![]() 產品
產品![]() 件(產品件數為整數件),根據以上信息解答下列問題:
件(產品件數為整數件),根據以上信息解答下列問題:
(1)生產![]() 兩種產品的方案有哪幾種?
兩種產品的方案有哪幾種?
(2)設生產這![]() 件產品可獲利
件產品可獲利![]() 元,寫出關于
元,寫出關于![]() 的函數解析式,寫出(1)中利潤最大的方案,并求出最大利潤.
的函數解析式,寫出(1)中利潤最大的方案,并求出最大利潤.
查看答案和解析>>
科目:初中數學 來源: 題型:
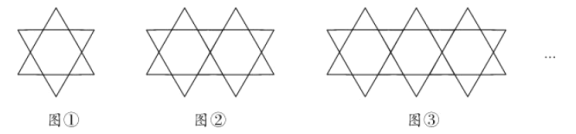
【題目】將大小相同的正三角形按如圖所示的規律拼圖案,其中第①個圖案中有6個小三角形和1個正六邊形;第②個圖案中有10個小三角形和2個正六邊形;第③個圖案中有14個小三角形和3個正六邊形;…;按此規律排列下去,已知一個正六邊形的面積為![]() ,一個小三角形的面積為
,一個小三角形的面積為![]() ,則第③個圖案中所有的小三角形和正六邊形的面積之和為______.(結果用含
,則第③個圖案中所有的小三角形和正六邊形的面積之和為______.(結果用含![]() 、
、![]() 的代數式表示)
的代數式表示)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC為直角三角形,∠C=90°,BC=2cm,∠A=30°,四邊形DEFG為矩形,DE=2![]() cm,EF=6cm,且點C、B、E、F在同一條直線上,點B與點E重合.Rt△ABC以每秒1cm的速度沿矩形DEFG的邊EF向右平移,當點C與點F重合時停止.設Rt△ABC與矩形DEFG的重疊部分的面積為ycm2,運動時間xs.能反映ycm2與xs之間函數關系的大致圖象是( )
cm,EF=6cm,且點C、B、E、F在同一條直線上,點B與點E重合.Rt△ABC以每秒1cm的速度沿矩形DEFG的邊EF向右平移,當點C與點F重合時停止.設Rt△ABC與矩形DEFG的重疊部分的面積為ycm2,運動時間xs.能反映ycm2與xs之間函數關系的大致圖象是( )

A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(感知)如圖①,點C是AB中點,CD⊥AB,P是CD上任意一點,由三角形全等的判定方法“SAS”易證△PAC≌△PBC,得到線段垂直平分線的一條性質“線段垂直平分線上的點到線段兩端的距離相等”

(探究)如圖②,在平面直角坐標系中,直線y=-![]() x+1分別交x軸、y軸于點A和點B,點C是AB中點,CD⊥AB交OA于點D,連結BD,求BD的長
x+1分別交x軸、y軸于點A和點B,點C是AB中點,CD⊥AB交OA于點D,連結BD,求BD的長
(應用)如圖③
(1)將線段AB繞點A順時針旋轉90°得到線段AB′,請在圖③網格中畫出線段AB;
(2)若存在一點P,使得PA=PB′,且∠APB′≠90°,當點P的橫、縱坐標均為整數時,則AP長度的最小值為______.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】“大美濕地,水韻鹽城”.某校數學興趣小組就“最想去的鹽城市旅游景點”隨機調查了本校部分學生,要求每位同學選擇且只能選擇一個最想去的景點,下面是根據調查結果進行數據整理后繪制出的不完整的統計圖:

請根據圖中提供的信息,解答下列問題:
(1)求被調查的學生總人數;
(2)補全條形統計圖,并求扇形統計圖中表示“最想去景點D”的扇形圓心角的度數;
(3)若該校共有800名學生,請估計“最想去景點B“的學生人數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】解放橋是天津市的標志性建筑之一,是一座全鋼結構的部分可開啟的橋梁,
(I)如圖①,已知解放橋可開啟部分的橋面的跨度AB等于47m,從AB的中點C處開啟,則AC開啟至A'C'的位置時,A'C'的長為 .
(II)如圖②,某校數學興趣小組要測量解放橋的全長PQ,在觀景平臺M處測得∠PMQ=54°,沿河岸MQ前行,在觀景平臺N處測得∠PNQ=73°。已知PQ⊥MQ,MN=40m,求解放橋的全長PQ(tan54°≈1.4,tan73°≈3.3,結果保留整數)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】今年4月22日是第50個世界地球日,某校在八年級5個班中,每班各選拔10名學生參加“環保知識競賽”并評出了一、二、三等獎各若干名,學校將獲獎情況繪成如圖所示的不完整的條形統計圖和扇形統計圖,請你根據圖中信息解答下列問題:
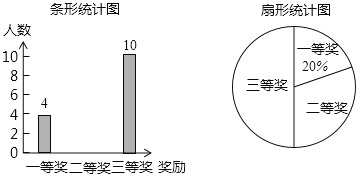
(1)求本次競賽獲獎的總人數,并補全條形統計圖;
(2)求扇形統計圖中“二等獎”所對應扇形的圓心角度數;
(3)已知甲、乙、丙、丁4位同學獲得一等獎,學校將采取隨機抽簽的方式在4人中選派2人參加上級團委組織的“愛護環境、保護地球”知識競賽,請求出抽到的2人恰好是甲和乙的概率(用畫樹狀圖或列表等方法求解).
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com