Question

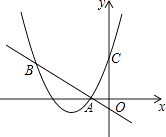
【題目】如圖，二次函數y=（x+2）2+m的圖象與y軸交于點C，點B在拋物線上，且與點C關于拋物線的對稱軸對稱，已知一次函數y=kx+b的圖象經過該二次函數圖象上的點A（﹣1，0）及點B．

（1）求二次函數與一次函數的解析式；
（2）根據圖象，寫出滿足（x+2）2+m≥kx+b的x的取值范圍．

Answer 1

【答案】
（1）解：∵拋物線y=（x+2）2+m經過點A（﹣1，0），

∴0=1+m，

∴m=﹣1，

∴拋物線解析式為y=（x+2）2﹣1=x2+4x+3，

∴點C坐標（0，3），

∵對稱軸x=﹣2，B、C關于對稱軸對稱，

∴點B坐標（﹣4，3），

∵y=kx+b經過點A、B，

∴ ，解得 ，

∴一次函數解析式為y=﹣x﹣1

（2）解：由圖象可知，寫出滿足（x+2）2+m≥kx+b的x的取值范圍為x≤﹣4或x≥﹣1．

【解析】（1）先利用待定系數法先求出m，再求出點B坐標，利用方程組求出一次函數解析式．（2）根據二次函數的圖象在一次函數的圖象上面即可寫出自變量x的取值范圍．
【考點精析】解答此題的關鍵在于理解確定一次函數的表達式的相關知識，掌握確定一個一次函數，需要確定一次函數定義式y=kx+b（k不等于0）中的常數k和b．解這類問題的一般方法是待定系數法．