
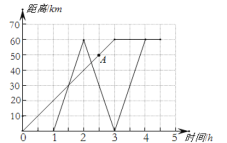
【題目】小南一家到某度假村度假.小南和媽媽坐公交車先出發,爸爸自駕車沿著相同的道路后出發.爸爸到達度假村后,發現忘了東西在家里,于是立即返回家里取,取到東西后又馬上駕車前往度假村(取東西的時間忽略不計).如下圖是他們離家的距離s(km)與小南離家的時間t(h)的關系圖.請根據圖回答下列問題:
(1)圖中的自變量是_________,因變量是_________,小南家到該度假村的距離是_____km.
(2)小南出發___________小時后爸爸駕車出發,爸爸駕車的平均速度為___________km/h,圖中點A表示 .
(3)小南從家到度假村的路途中,當他與爸爸相遇時,離家的距離約是___________km.
【答案】(1)t,s,60;(2) 1,60,小南出發2.5小時后,離家的距離為50km ;(3)30或45.
【解析】
(1)直接利用常量與變量的定義得出答案;直接利用函數圖象結合縱坐標得出答案;
(2)利用函數圖象求出爸爸晚出發1小時,根據速度=路程÷時間求解即可;根據函數圖象的橫縱坐標的意義得出A點的意義;
(3)利用函數圖象得出交點的位置進而得出答案.
(1)自變量是時間或t,因變量是距離或s;小亮家到該度假村的距離是:60;
(2)小亮出發1小時后爸爸駕車出發:爸爸駕車的平均速度為60÷1=km/h; 圖中點A表示:小亮出發2.5小時后,離度假村的距離為10km;
(3)當20t=60(t-1),解得:t=1.5
則離家20×1.5=30(千米)
當20t=120-60(t-1),解得:t=2.25
則離家20×2.25=45(千米)
小亮從家到度假村的路途中,當他與他爸爸相遇時.離家的距離約是30或45.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】我們約定:體重在選定標準的![]() %(包含)范圍之內時都稱為“一般體重”.為了解某校七年級男生中具有“一般體重”的人數,我們從該校七年級男生中隨機選出10名男生,測量出他們的體重(單位:kg),收集并整理得到如下統計表:
%(包含)范圍之內時都稱為“一般體重”.為了解某校七年級男生中具有“一般體重”的人數,我們從該校七年級男生中隨機選出10名男生,測量出他們的體重(單位:kg),收集并整理得到如下統計表:
男生序號 | ① | ② | ③ | ④ | ⑤ | ⑥ | ⑦ | ⑧ | ⑨ | ⑩ |
體重 | 45 | 62 | 55 | 58 | 67 | 80 | 53 | 65 | 60 | 55 |
根據以上表格信息解決如下問題:
(1)將這組數據的三個統計量:平均數、中位數和眾數填入下表:
平均數 | 中位數 | 眾數 |
(2)請你選擇其中一個統計量作為選定標準,說明選擇的理由.并按此選定標準找出這10名男生中具有“一般體重”的男生.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】完成下面的證明.
已知:如圖,![]() ,
,![]() .
.
求證:![]() .
.
證明:∵![]() ,
,
∴![]() __________(_______________________________________).
__________(_______________________________________).
∴![]() (_____________________________________________).
(_____________________________________________).
∵![]() ,
,
∴_______![]()
∴![]() (______________________________________).
(______________________________________).

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,三角形![]() (記作
(記作![]() )在方格中,方格紙中的每個小方格都是邊長為1個單位的正方形,三個頂點的坐標分別是
)在方格中,方格紙中的每個小方格都是邊長為1個單位的正方形,三個頂點的坐標分別是![]() ,
,![]() ,
,![]() ,先將
,先將![]() 向上平移3個單位長度,再向右平移2個單位長度,得到
向上平移3個單位長度,再向右平移2個單位長度,得到![]() .
.

(1)在圖中畫出![]() ;
;
(2)點![]() ,
,![]() ,
,![]() 的坐標分別為______、________、_________;
的坐標分別為______、________、_________;
(3)若![]() 有一點
有一點![]() ,使
,使![]() 與
與![]()
![]() 面積相等,求出
面積相等,求出![]() 點的坐標.
點的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為響應國家的“一帶一路”經濟發展戰略,樹立品牌意識,我市質檢部門對A、B、C、D四個廠家生產的同種型號的零件共2000件進行合格率檢測,通過檢測得出C廠家的合格率為95%,并根據檢測數據繪制了如圖1、圖2兩幅不完整的統計圖.
(1)抽查D廠家的零件為 件,扇形統計圖中D廠家對應的圓心角為 ;
(2)抽查C廠家的合格零件為 件,并將圖1補充完整;
(3)通過計算說明合格率排在前兩名的是哪兩個廠家;
(4)若要從A、B、C、D四個廠家中,隨機抽取兩個廠家參加德國工業產品博覽會,請用“列表法”或“畫樹形圖”的方法求出(3)中兩個廠家同時被選中的概率.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,在△ABC中,∠BAC=90°,AB=AC,直線MN過點A,且MN∥BC,點D是直線MN上一點,不與點A重合.若點E是線段AB上一點,且DE=DA.
(1)請說明線段DE⊥DA.
(2)如圖2,連接BD,過點D作DP⊥DB交線段AC于點P,請判斷線段DB與DP的數量關系,并說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
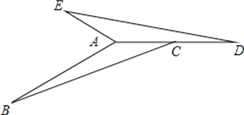
【題目】在△ABC中,∠B+∠ACB=30°,AB=4,△ABC逆時針旋轉一定角度后與△ADE重合,且點C恰好成為AD中點,如圖
(1)指出旋轉中心,并求出旋轉角的度數.
(2)求出∠BAE的度數和AE的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】對于平面直角坐標系![]() 中的點
中的點![]() ,若點
,若點![]() 的坐標為
的坐標為![]() (其 中
(其 中![]() 為常數, 且
為常數, 且![]() ,則稱點
,則稱點![]() 為點
為點![]() 的“
的“![]() 屬派生點” . 例如:
屬派生點” . 例如:![]() 的“ 2 屬派生點”為
的“ 2 屬派生點”為![]() ,即
,即![]() .
.
(Ⅰ) 點![]() 的“ 3 屬派生點”
的“ 3 屬派生點” ![]() 的坐標為 ;
的坐標為 ;
(Ⅱ) 若點![]() 的“ 5 屬派生點”
的“ 5 屬派生點” ![]() 的坐標為
的坐標為![]() ,求點
,求點![]() 的坐標;
的坐標;
(Ⅲ) 若點![]() 在
在![]() 軸的正半軸上, 點
軸的正半軸上, 點![]() 的“
的“![]() 屬派生點”為
屬派生點”為![]() 點, 且線段
點, 且線段![]() 的長度為線段
的長度為線段![]() 長度的 2 倍, 求
長度的 2 倍, 求![]() 的值 .
的值 .
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com