
【題目】數(shù)學(xué)綜合實(shí)踐課上,老師提出問(wèn)題:如圖,有一張長(zhǎng)為![]() ,寬為
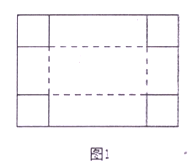
,寬為![]() 的長(zhǎng)方形紙板,在紙板四個(gè)角剪去四個(gè)相同的小正方形,然后把四邊折起來(lái)(實(shí)線為剪裁線,虛線為折疊線),做成一個(gè)無(wú)蓋的長(zhǎng)方體盒子,問(wèn)小正方形的邊長(zhǎng)為多少時(shí),盒子的體積最大?為了解決這個(gè)問(wèn)題,小明同學(xué)根據(jù)學(xué)習(xí)函數(shù)的經(jīng)驗(yàn),進(jìn)行了如下的探究:
的長(zhǎng)方形紙板,在紙板四個(gè)角剪去四個(gè)相同的小正方形,然后把四邊折起來(lái)(實(shí)線為剪裁線,虛線為折疊線),做成一個(gè)無(wú)蓋的長(zhǎng)方體盒子,問(wèn)小正方形的邊長(zhǎng)為多少時(shí),盒子的體積最大?為了解決這個(gè)問(wèn)題,小明同學(xué)根據(jù)學(xué)習(xí)函數(shù)的經(jīng)驗(yàn),進(jìn)行了如下的探究:
(1)設(shè)小正方形的邊長(zhǎng)為![]() ,長(zhǎng)方體體積為
,長(zhǎng)方體體積為![]() ,根據(jù)長(zhǎng)方體的體積公式,可以得到
,根據(jù)長(zhǎng)方體的體積公式,可以得到![]() 與
與![]() 的函數(shù)關(guān)系式是 ,其中自變量
的函數(shù)關(guān)系式是 ,其中自變量![]() 的取值范圍是 ;
的取值范圍是 ;
(2)列出![]() 與
與![]() 的幾組對(duì)應(yīng)值如下表:
的幾組對(duì)應(yīng)值如下表:
| … |
|
|
|
|
|
|
| 1 |
|
| … |
| … | 1.3 | 2.2 | 2.7 | 3.0 | 2.8 | 2.5 | 1.5 | 0.9 | … |
(注:補(bǔ)全表格,保留1位小數(shù)點(diǎn))
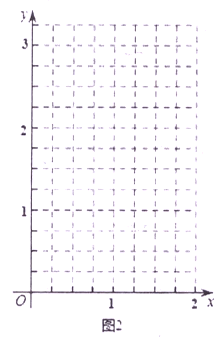
(3)如圖,請(qǐng)?jiān)谄矫嬷苯亲鴺?biāo)系中描出以補(bǔ)全后表格中各對(duì)對(duì)應(yīng)值為坐標(biāo)的點(diǎn),畫(huà)出該函數(shù)圖象;
(4)結(jié)合函數(shù)圖象回答:當(dāng)小正方形的邊長(zhǎng)約為 ![]() 時(shí),無(wú)蓋長(zhǎng)方體盒子的體積最大,最
時(shí),無(wú)蓋長(zhǎng)方體盒子的體積最大,最
大值約為 .
【答案】(1)![]() ;0﹤
;0﹤![]() ﹤
﹤![]() (2)3.0;2.0(3)見(jiàn)詳解(4)0.55;3.03
(2)3.0;2.0(3)見(jiàn)詳解(4)0.55;3.03
【解析】
(1)根據(jù)題意,列出y與x的函數(shù)關(guān)系式,根據(jù)盒子長(zhǎng)、寬、高值為正數(shù),求出自變量的取值范圍;
(2)把![]() =
=![]() ,
,![]() =1分別代入(1)中所求的函數(shù)式,從而求出y的值;
=1分別代入(1)中所求的函數(shù)式,從而求出y的值;
(3)根據(jù)(2)求得的y的值補(bǔ)全表格,根據(jù)上表描點(diǎn)畫(huà)出圖象;
(4)利用(3)畫(huà)出的圖象求出盒子最大體積.
解:(1)由已知得,![]()
根據(jù)題意得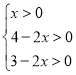 解得:0﹤
解得:0﹤![]() ﹤
﹤![]()
故答案為:![]() ,0﹤
,0﹤![]() ﹤
﹤![]()
(2)當(dāng)![]() =
=![]() 時(shí),y=
時(shí),y=![]() ×(4-2×
×(4-2×![]() )(3-2×
)(3-2×![]() )=3.0
)=3.0
當(dāng)![]() =1時(shí),y=1×(4-2×1)(3-2×1)=2.0
=1時(shí),y=1×(4-2×1)(3-2×1)=2.0
(3)補(bǔ)全表格如下表,
| … |
|
|
|
|
|
|
| 1 |
|
| … |
| … | 1.3 | 2.2 | 2.7 | 3.0 | 3.0 | 2.8 | 2.5 | 2.0 | 1.5 | 0.9 | … |
根據(jù)補(bǔ)全的表格畫(huà)出函數(shù)圖像,如下圖2
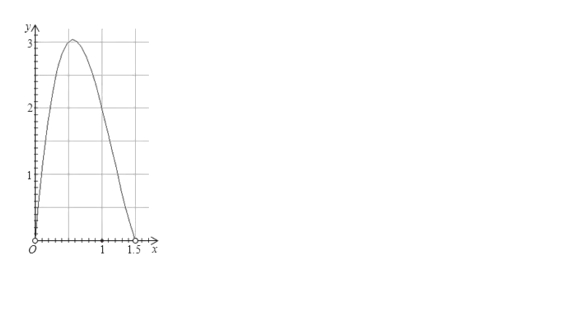
(4)根據(jù)圖像,當(dāng)![]() =0.55dm時(shí),盒子的體積最大,最大值約為3.03dm3
=0.55dm時(shí),盒子的體積最大,最大值約為3.03dm3


 文敬圖書(shū)課時(shí)先鋒系列答案
文敬圖書(shū)課時(shí)先鋒系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】某單位在疫情期間用3000元購(gòu)進(jìn)A、B兩種口罩1100個(gè),購(gòu)買(mǎi)A種口罩與購(gòu)買(mǎi)B種口罩的費(fèi)用相同,且A種口罩的單價(jià)是B種口罩單價(jià)的1.2倍;
(1)求A,B兩種口罩的單價(jià)各是多少元?
(2)若計(jì)劃用不超過(guò)7000元的資金再次購(gòu)進(jìn)A、B兩種口罩共2600個(gè),已知A、B兩種口罩的進(jìn)價(jià)不變,求A種口罩最多能購(gòu)進(jìn)多少個(gè)?
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】為了了解青少年形體情況,現(xiàn)隨機(jī)抽查了某市若十名初中學(xué)生坐必、站姿.走安的好壞情況我們對(duì)測(cè)評(píng)數(shù)據(jù)作了適當(dāng)處理(如果一個(gè)學(xué)生有一種以上:不良姿勢(shì).以他最突出的一種作記載) ,并將統(tǒng)計(jì)結(jié)果繪制了如下兩幅不完整的統(tǒng)計(jì)圖.請(qǐng)你根據(jù)圖中所給信息解答下列問(wèn)題:
![]() 求這次抽查一共抽查了多少名學(xué)生;
求這次抽查一共抽查了多少名學(xué)生;
![]() 請(qǐng)將條形統(tǒng)計(jì)圖補(bǔ)充完整;
請(qǐng)將條形統(tǒng)計(jì)圖補(bǔ)充完整;
![]() 如果全市有
如果全市有![]() 萬(wàn)名初中生,那么全市初中生中,三姿良好的學(xué)生約有多少名
萬(wàn)名初中生,那么全市初中生中,三姿良好的學(xué)生約有多少名

查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,一次函數(shù)y=kx+b的圖象與反比例函數(shù)y=![]() (x>0)的圖象交于點(diǎn)P(n,2),與x軸交于點(diǎn)A(-4,0),與y軸交于點(diǎn)C,PB丄x軸于點(diǎn)B,點(diǎn)A與點(diǎn)B關(guān)于y軸對(duì)稱(chēng).
(x>0)的圖象交于點(diǎn)P(n,2),與x軸交于點(diǎn)A(-4,0),與y軸交于點(diǎn)C,PB丄x軸于點(diǎn)B,點(diǎn)A與點(diǎn)B關(guān)于y軸對(duì)稱(chēng).

(1)求一次函數(shù)、反比例函數(shù)的解析式;
(2)求證:點(diǎn)C為線段AP的中點(diǎn);
(3)反比例函數(shù)圖象上是否存在點(diǎn)D,使四邊形BCPD為菱形,如果存在,說(shuō)明理由并求出點(diǎn)D的坐標(biāo);如果不存在,說(shuō)明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
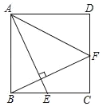
【題目】如圖,在正方形ABCD中,點(diǎn)E是BC上一點(diǎn),BF⊥AE交DC于點(diǎn)F,若AB=5,BE=2,則AF=____.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】某校九年級(jí)開(kāi)展征文活動(dòng),征文主題只能從“愛(ài)國(guó)”“敬業(yè)”“誠(chéng)信”“友善”四個(gè)主題中選擇一個(gè),九年級(jí)每名學(xué)生按要求都上交了一份征文,學(xué)校為了解選擇各種征文主題的學(xué)生人數(shù),隨機(jī)抽取了部分征文進(jìn)行了調(diào)查,根據(jù)調(diào)查結(jié)果繪制成如下兩幅不完整的統(tǒng)計(jì)圖.
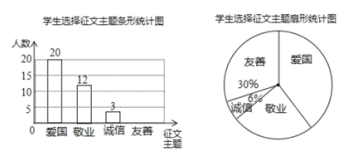
(1)求本次調(diào)查共抽取了多少名學(xué)生的征文;
(2)將上面的條形統(tǒng)計(jì)圖和扇形統(tǒng)計(jì)圖補(bǔ)充完整;
(3)本次抽取的3份以“誠(chéng)信”為主題的征文分別是小義、小玉和大力的,若從中隨機(jī)選取2份以“誠(chéng)信”為主題的征文進(jìn)行交流,請(qǐng)用畫(huà)樹(shù)狀圖法或列表法求小義和小玉同學(xué)的征文同時(shí)被選中的概率.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
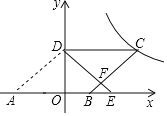
【題目】如圖,在平面直角坐標(biāo)系中,O為坐標(biāo)原點(diǎn),ABCD的邊AB在x軸上,頂點(diǎn)D在y軸的正半軸上,點(diǎn)C在第一象限,將△AOD沿y軸翻折,使點(diǎn)A落在x軸上的點(diǎn)E處,點(diǎn)B恰好為OE的中點(diǎn),DE與BC交于點(diǎn)F.若y![]() (k≠0)圖象經(jīng)過(guò)點(diǎn)C,且S△BEF=1,則k的值為________.
(k≠0)圖象經(jīng)過(guò)點(diǎn)C,且S△BEF=1,則k的值為________.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
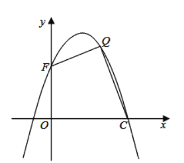
【題目】如圖,拋物線![]() 與直線
與直線![]() 相交于
相交于![]() ,
,![]() 兩點(diǎn),且拋物線經(jīng)過(guò)點(diǎn)
兩點(diǎn),且拋物線經(jīng)過(guò)點(diǎn)![]()

(1)求拋物線的解析式.
(2)點(diǎn)![]() 是拋物線上的一個(gè)動(dòng)點(diǎn)(不與點(diǎn)
是拋物線上的一個(gè)動(dòng)點(diǎn)(不與點(diǎn)![]() 點(diǎn)
點(diǎn)![]() 重合),過(guò)點(diǎn)
重合),過(guò)點(diǎn)![]() 作直線
作直線![]() 軸于點(diǎn)
軸于點(diǎn)![]() ,交直線
,交直線![]() 于點(diǎn)
于點(diǎn)![]() .當(dāng)
.當(dāng)![]() 時(shí),求
時(shí),求![]() 點(diǎn)坐標(biāo);
點(diǎn)坐標(biāo);
(3)如圖所示,設(shè)拋物線與![]() 軸交于點(diǎn)
軸交于點(diǎn)![]() ,在拋物線的第一象限內(nèi),是否存在一點(diǎn)
,在拋物線的第一象限內(nèi),是否存在一點(diǎn)![]() ,使得四邊形
,使得四邊形![]() 的面積最大?若存在,請(qǐng)求出點(diǎn)
的面積最大?若存在,請(qǐng)求出點(diǎn)![]() 的坐標(biāo);若不存在,說(shuō)明理由.
的坐標(biāo);若不存在,說(shuō)明理由.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話(huà):027-86699610 舉報(bào)郵箱:58377363@163.com