
【題目】2020年春節前夕“新型冠狀病毒”爆發.疫情就是命令,防控就是使命.全國各地馳援武漢的醫護工作者,踐行醫者仁心的使命與擔當舍小家,為大家,用自己的專業知識與血肉之軀構筑起全社會抗擊疫情的鋼鐵長城.下面是2月9日當天全國部分省市馳援武漢醫護工作者的人數統計圖(不完整).
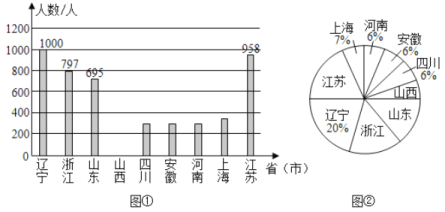
請解答下列問題:
(1)①上述省市2月9日當天馳援武漢的醫護工作者的總人數為_____人;
②請將條形統計圖補充完整;
(2)請求出扇形統計圖中“山西”所對應扇形的圓心角的度數;
(3)本次山西馳援武漢的醫護工作者中,有5人報名去重癥區,王醫生和李醫生就在其中,若從報名的5人中隨機安排2人,求同時安排王醫生和李醫生的概率.
【答案】(1)①5000;②詳見解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)①根據遼寧的人數和所占的百分比求出2月9日當天馳援武漢的醫護工作者的總人數;
②先求出江蘇、浙江和山東所占的百分比,再用整體1減去各省份所占的百分比,求出山西所占的百分比,再用總人數乘以山西所占的百分比即可補全統計圖;
(2)用山西所占的百分比乘以360°即可得出答案;
(3)根據題意畫出樹狀圖得出所有等情況數和同時安排王醫生和李醫生的情況數,然后根據概率公式即可得出答案.
(1)①2月9日當天馳援武漢的醫護工作者的總人數為:1000÷20%=5000(人),
②江蘇所占的百分比是:![]() ×100%=19.16%;
×100%=19.16%;
浙江所占的百分比是:![]() ×100%=15.94%;
×100%=15.94%;
山東所占的百分比是:![]() ×100%=13.9%;
×100%=13.9%;
則山西所占的百分比是:1-19.16%-7%-6%-6%-6%-13.9%-15.94%-20%=6%,
山西的人數是5000×6%=300(人),補圖如下:
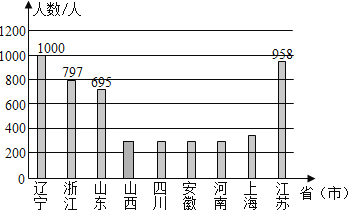
故答案為:5000;
(2)“山西”所對應扇形的圓心角的度數是360°×6%=21.6°;(3)這5名醫護工作者分別用1,2,3,4,5表示,其中王醫生用1表示,李醫生用2表示,根據題意畫圖如下:
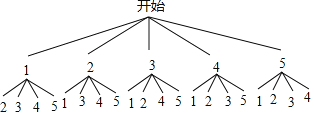
共有20種等情況數,其中同時安排王醫生和李醫生的有2種,
則同時安排王醫生和李醫生的概率![]() .
.


 小學學習好幫手系列答案
小學學習好幫手系列答案 小學同步三練核心密卷系列答案
小學同步三練核心密卷系列答案科目:初中數學 來源: 題型:
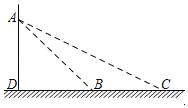
【題目】如圖,一輛轎車在經過某路口的感應線B和C處時,懸臂燈桿上的電子警察拍攝到兩張照片,兩感應線之間距離BC為6.2m,在感應線B、C兩處測得電子警察A的仰角分別為∠ABD=45°,∠ACD=28°.求電子警察安裝在懸臂燈桿上的高度AD的長.(結果精確到0.1米)(參考數據:sin28°=0.47,cos28°=0.88,tan28°=0.53)
查看答案和解析>>
科目:初中數學 來源: 題型:
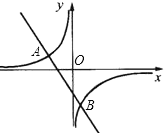
【題目】如圖,一次函數y=kx+b的圖象與反比例函數y=![]() 的圖象交于A(﹣2,1),B(1,n)兩點.
的圖象交于A(﹣2,1),B(1,n)兩點.
(1)求反比例函數和一次函數的解析式;
(2)根據圖象寫出使一次函數的值>反比例函數的值的x的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
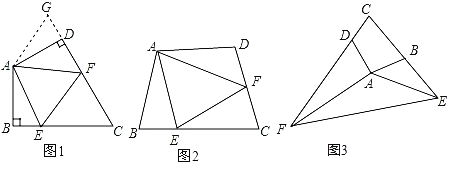
【題目】(1)如圖1:在四邊形ABC中,AB=AD,∠B=∠ADC=90°,E、F分別是BC、CD上的點,且EF=BE+FD,探究圖中∠BAE、∠FAD、∠EAF之間的數量關系.小王同學探究此問題的方法是:延長FD到點G,使DG=BE.連接AG,先證明△ABE≌△ADG,再證明△AEF≌△AGF,可得出結論,他的結論應是 ;
(2)如圖2,若在四邊形ABCD中,AB=AD,∠B+∠D=180°.E、F分別是BC、CD上的點,且EF=BE+FD,上述結論是否仍然成立,并說明理由;
(3)如圖3,已知在四邊形ABCD中,∠ABC+∠ADC=180°AB=AD,若點E在CB的延長線上,點F在CD的延長線上,如圖3所示,仍然滿足EF=BE+FD,請寫出∠EAF與∠DAB的數量關系,并給出證明過程.
查看答案和解析>>
科目:初中數學 來源: 題型:
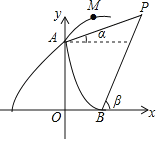
【題目】如圖是某導彈發射車在山頂A處進行射擊訓練的示意圖,點A在y軸上,與原點O的距離是8百米(為了計算方便,我們把本題中的距離用百米作單位).此導彈發射車在A處進行某個角度的射擊訓練,點M是導彈向右上射出后某時刻的位置.忽略空氣阻力,實驗表明:導彈射出t秒時,點M,A的水平距離是vt百米,點M與x軸(水平)的豎直距離是(8+vt﹣5t2)百米(v的值由發射者設定).在點A和x軸上的點B處觀測射擊目標P的仰角分別是a和β,OB=3百米,tanα=![]() .tanβ=
.tanβ=![]() .
.
(1)若v=7,完成下列問題:
①當點M,A的水平距離是7百米時,點M到x軸的距離是 百米;
②設點M坐標為(x,y),求y與x的關系式(不必寫x的取值范圍).
(2)按(1)的射擊方式,能否命中目標P?請說明理由.
(3)目標以m百米/秒的速度從點P向右移動,當v![]() 時,若能使目標被擊中,求m的取值范圍.
時,若能使目標被擊中,求m的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】綜合與探究
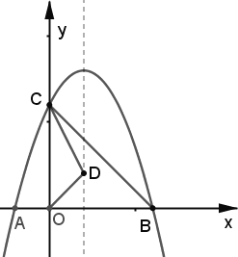
如圖,拋物線![]() 與
與![]() 軸交于
軸交于![]() 兩點(點
兩點(點![]() 在點
在點![]() 的左側),與
的左側),與![]() 軸交于點
軸交于點![]() ,連接
,連接![]() ,點
,點![]() 為拋物線對稱軸上一動點.
為拋物線對稱軸上一動點.
(1)求直線![]() 的函數表達式;
的函數表達式;
(2)連接![]() ,求
,求![]() 周長的最小值;
周長的最小值;
(3)在拋物線上是否存在一點![]() .使以
.使以![]() 為頂點的四邊形是以
為頂點的四邊形是以![]() 為邊的平行四邊形?若存在,請直接寫出
為邊的平行四邊形?若存在,請直接寫出![]() 點的坐標;若不存在,請說明理由.
點的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
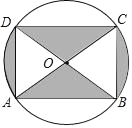
【題目】如圖是某商品的標志圖案,AC與BD是⊙O的兩條直徑,首尾順次連接點A、B、C、D,得到四邊形ABCD,若AC=10cm,∠BAC=36°,則圖中陰影部分的面積為_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校開展了“互助、平等、感恩、和諧、進取”主題班會活動,活動后,就活動的![]() 個主題進行了抽樣調查(每位同學只選最關注的一個),根據調查結果繪制了兩幅不完整的統計圖.根據圖中提供的信息,解答下列問題:
個主題進行了抽樣調查(每位同學只選最關注的一個),根據調查結果繪制了兩幅不完整的統計圖.根據圖中提供的信息,解答下列問題:
(1)這次調查的學生共有多少名?
(2)請將條形統計圖補充完整,并在扇形統計圖中計算出“進取”所對應的圓心角的度數.
(3)如果要在這![]() 個主題中任選兩個進行調查,根據(2)中調查結果,用樹狀圖或列表法,求恰好選到學生關注最多的兩個主題的概率(將互助、平等、感恩、和諧、進取依次記為A、B、C、D、E).
個主題中任選兩個進行調查,根據(2)中調查結果,用樹狀圖或列表法,求恰好選到學生關注最多的兩個主題的概率(將互助、平等、感恩、和諧、進取依次記為A、B、C、D、E).

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC中,∠ABC=∠ACB,點D在BC所在的直線上,點E在射線AC上,且AD=AE,連接DE.
⑴如圖①,若∠B=∠C=35°,∠BAD=80°,求∠CDE的度數;
⑵如圖②,若∠ABC=∠ACB=75°,∠CDE=18°,求∠BAD的度數;
⑶當點D在直線BC上(不與點B、C重合)運動時,試探究∠BAD與∠CDE的數量關系,并說明理由.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com