題目列表(包括答案和解析)
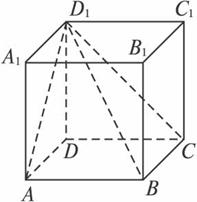
正方體ABCD—A1B1C1D1的棱長為1，E、F、G分別為棱AA1、CC1、A1B1的中點，則下列幾個命題：
①在空間中與三條直線A1D1，EF，CD都相交的直線有無數條;
②點G到平面ABC1D1的距離為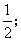
③直線AA1與平面ABC1D1所成的角等于45°；
④空間四邊形ABCD1在正方體六個面內形成六個射影，其面積的最小值是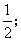
⑤直線A1C1與直線AG所成角的余弦值為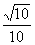
;
⑥若一直線PQ既垂直于A1D,又垂直于AC,則直線PQ與BD1是垂直不相交的關系．
其中真命題是 ．（寫出所有真命題的序號）
| 1 |
| 2 |
| 1 |
| 2 |
3
| ||
| 10 |
| 5π |
| 6 |
正方體ABCD－A1B1C1D1的棱長為1，E為A1B1的中點，則下列五個命題：
①點E到平面ABC1D1的距離為
②直線BC與平面ABC1D1所成的角等于45°；
③空間四邊形ABCD1在正方體六個面內形成六個射影，其面積的最小值是
④AE與DC1所成的角為
；
⑤二面角A－BD1－C的大小為
．
其中真命題是________．(寫出所有真命題的序號)
①點E到平面ABC1D1的距離為
;②直線BC與平面ABC1D1所成的角等于45°;③空間四邊形ABCD1在正方體六個面內射影的面積的最小值為
;④BE與CD1所成的角為arcsin
.
其中真命題的編號是 (寫出所有真命題的編號).?
①點E到平面ABC1D1的距離為
;
②直線BC與平面ABC1D1所成的角等于45°;
③空間四邊形ABCD1在正方體六個面內的射影圍成的圖形中,面積最小的值為
;
④BE與CD1所成角為arcsin
;
⑤二面角ABD1C的大小為
.
其中真命題是.(寫出所有真命題的序號)
一、選擇題: BBDBA BBBCB AC
二、填空題: 13.6
14.
15.1 16. ②③
三．解答題：本大題共6小題，共70分．解答應寫出文字說明，證明過程或演算步驟．
17．
解：（1）∵ 
, 且與向量
所成角為
∴ 
， ∴ 
，
又
，∴ 
，即
。
（2）由（1）可得：
∴ 
∵ 
，
∴ 
，
∴ 
，
∴ 當
=1時，A=
∴AB=2，
則
18．解：（1）P=
（2）隨機變量
的取值為0, 1, 2, 3.
由n次獨立重復試驗概率公式
得
隨機變量的分布列是
0
1
2
3
的數學期望是 
19．證明(Ⅰ)
AB∥DC，
DC
平面PAD．
DCPD
DCAD，
PDA為二面角P－CD－B的平面角．
故
PDA＝45° PA＝AD＝3，
APD＝45°． PAAD．
又PAAB ，PA平面ABCD．
（Ⅱ）證法一：延長DA，CE交于點N，連結PN,
由折疊知
又
．
，
又由（１）知
，
為二面角
的平面角．………9分
在直角三角形
中，
，
．
即平面PEC和平面PAD所成銳二面角為30°．
證法二：如圖建立空間直角坐標系
，
則
，
設
為平面
的法向量，則
，可設
，又平面
的法向量
，
．
．
20．解：（I）依題意得
（II）依題意得，
上恰有兩個相異實根，
令
故
在[0，1]上是減函數，在
上是增函數，
21．解：（1）直線
方程為
與
聯立得
（2）設弦AB的中點M的坐標為
依題意有
所以弦AB的中點M的軌跡是以
為中心，
焦點在
軸上，長軸長為1，短軸長為
的橢圓。
（3）設直線AB的方程為
代入
整理得
直線AB過橢圓的左焦點F，方程有兩個不等實根。
記
中點
則
的垂直平分線NG的方程為
令
得
點G橫坐標的取值范圍為
22．解：（I）把
（II）
， ①
②
①式減②式得，
， 變形得
，
又因為
時上式也成立。
所以，數列
為公比的等比數列，
所以
（III）
，
所以
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com