
題目列表(包括答案和解析)
運用數學歸納法證明命題要分兩步走.第一步是遞推的_________;第二步是遞推的________,這兩步是缺一不可的.
證明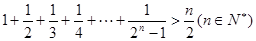 時,假設當
時,假設當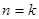 時成立,則當
時成立,則當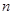
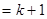 時,左邊增加的項數為(
)
時,左邊增加的項數為(
)
A.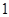 B.
B.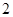
 C.
C.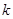 D.
D.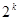
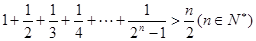 時,假設當
時,假設當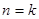 時成立,則當
時成立,則當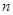
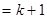 時,左邊增加的項數為( )
時,左邊增加的項數為( )A.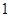 | B.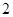  | C.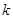 | D.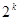 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 2n-1 |
| n |
| 2 |
(1)當![]() 時,等式
時,等式![]()
是否成立?![]() 呢?
呢?
(2)假設![]() 時,等式
時,等式![]() 成立.
成立.
能否推得![]() 時,等式也成立?
時,等式也成立?![]() 時等式成立嗎?
時等式成立嗎?
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com