題目列表(包括答案和解析)
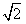a，
A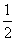B；②AB=
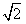a；③CM⊥AB；④BC⊥AC。請你從中再選擇兩個條件以確定cosθ的值，并求解．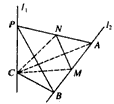 
如圖,已知圓錐體
的側面積為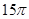
，底面半徑
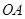和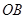
互相垂直，且
，
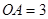是母線
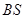的中點.
（1）求圓錐體的體積；
（2）異面直線與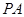
所成角的大小（結果用反三角函數表示）．
【解析】本試題主要考查了圓錐的體積和異面直線的所成的角的大小的求解。
第一問中，由題意，
得
，故
從而體積
.2中取OB中點H，聯結PH,AH.
由P是SB的中點知PH//SO，則
(或其補角)就是異面直線SO與PA所成角.
由SO
平面OAB,
PH平面OAB,PHAH.在
OAH中，由OAOB得
；
在
中，
，PH=1/2SB=2，，
則
，所以異面直線SO與P成角的大arctan
解：（1）由題意，得，
故從而體積.
（2）如圖2，取OB中點H，聯結PH,AH.
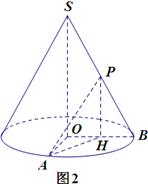
由P是SB的中點知PH//SO，則(或其補角)就是異面直線SO與PA所成角.
由SO平面OAB,PH平面OAB,PHAH.
在OAH中，由OAOB得；
在中，，PH=1/2SB=2，，
則，所以異面直線SO與P成角的大arctan
零件直徑相等的概率。本小題主要考查用列舉法計算隨機事件所含的基本事件數及事件發生的概率等基礎知識，考查數據處理能力及運用概率知識解決簡單的實際問題的能力。滿分12分
【解析】（Ⅰ）解：由所給數據可知，一等品零件共有6個.設“從10個零件中，隨機抽取一個為一等品”為事件A，則P（A）=
=
.
（Ⅱ）（i）解：一等品零件的編號為
.從這6個一等品零件中隨機抽取2個，所有可能的結果有：
,
,
,
,
,
,
共有15種.
(ii)解：“從一等品零件中，隨機抽取的2個零件直徑相等”（記為事件B）的所有可能結果有：
，
，共有6種.
所以P(B)=
.
（本小題滿分12分）
如圖，在五面體ABCDEF中，四邊形ADEF是正方形，FA⊥平面ABCD，BC∥AD，CD=1，AD=
，∠BAD＝∠CDA＝45°.
（Ⅰ）求異面直線CE與AF所成角的余弦值；
（Ⅱ）證明CD⊥平面ABF；
（Ⅲ）求二面角B-EF-A的正切值。
零件直徑相等的概率。本小題主要考查用列舉法計算隨機事件所含的基本事件數及事件發生的概率等基礎知識，考查數據處理能力及運用概率知識解決簡單的實際問題的能力。滿分12分
【解析】（Ⅰ）解：由所給數據可知，一等品零件共有6個.設“從10個零件中，隨機抽取一個為一等品”為事件A，則P（A）=
=
.
（Ⅱ）（i）解：一等品零件的編號為
.從這6個一等品零件中隨機抽取2個，所有可能的結果有：
,
,
,
,
,
,
共有15種.
(ii)解：“從一等品零件中，隨機抽取的2個零件直徑相等”（記為事件B）的所有可能結果有：
，
，共有6種.
所以P(B)=
.
（本小題滿分12分）
如圖，在五面體ABCDEF中，四邊形ADEF是正方形，FA⊥平面ABCD，BC∥AD，CD=1，AD=
，∠BAD＝∠CDA＝45°.
（Ⅰ）求異面直線CE與AF所成角的余弦值；
（Ⅱ）證明CD⊥平面ABF；
（Ⅲ）求二面角B-EF-A的正切值。
（本小題滿分12分）
有編號為
,
,…
的10個零件，測量其直徑（單位：cm），得到下面數據：
其中直徑在區間[1.48，1.52]內的零件為一等品。
（Ⅰ）從上述10個零件中，隨機抽取一個，求這個零件為一等品的概率；
（Ⅱ）從一等品零件中，隨機抽取2個.
（ⅰ）用零件的編號列出所有可能的抽取結果；
（ⅱ）求這2個零件直徑相等的概率。本小題主要考查用列舉法計算隨機事件所含的基本事件數及事件發生的概率等基礎知識，考查數據處理能力及運用概率知識解決簡單的實際問題的能力。滿分12分
【解析】（Ⅰ）解：由所給數據可知，一等品零件共有6個.設“從10個零件中，隨機抽取一個為一等品”為事件A，則P（A）=
=
.
（Ⅱ）（i）解：一等品零件的編號為
.從這6個一等品零件中隨機抽取2個，所有可能的結果有：
,
,
,
,
,
,
共有15種.
(ii)解：“從一等品零件中，隨機抽取的2個零件直徑相等”（記為事件B）的所有可能結果有：
，
，共有6種.
所以P(B)=
.
（本小題滿分12分）
如圖，在五面體ABCDEF中，四邊形ADEF是正方形，FA⊥平面ABCD，BC∥AD，CD=1，AD=
，∠BAD＝∠CDA＝45°.
（Ⅰ）求異面直線CE與AF所成角的余弦值；
（Ⅱ）證明CD⊥平面ABF；
一、 填空題：
1、
2、
3、128 4、
5、64 6、
7、
8、
9、-4 10、15 11、
12、（1）（2）（5）
二、選擇題：
13、D 14、 C 15、 B 16、 C
17、解：以A為原點，以AB、AD、AP所在直線分別
軸，
建立空間直角坐標系。 -----2分
則 C（2，1，0） N（1，0，1） 
=（-1，-1，1）---4分
D（0，2，0） M（1，
，1） 
=（1，-
，1）---6分
設與的夾角為
，
----8分
---10分
異面直線
與
所成的角為 -----12分
18、解：延長
，作
交于D，------4分
設
，則
------8分
解得
．------10分
故船繼續朝原方向前進有觸礁的危險．-----12
19、解： (1)因為f(x+y)=f(x)+f(y)，
令x=y=0，代入①式，-----2分
得f(0+0)=f(0)+f(0)，即 f(0)=0 --------4分
（２）令y=-x，代入①式，得 f(x-x)=f(x)+f(-x)，又f(0)=0，
則有0=f(x)+f(-x)．------6分
即f(-x)=-f(x)對任意x∈R成立，
所以f(x)是奇函數．．．．．．．8分
(3) f(3)=log
3＞0，即f(3)＞f(0)，
又f(x)在R上是單調函數，所以f(x)在R上是增函數，----10分
又由(1)f(x)是奇函數．
f(k?3
)＜-f(3-9-2)=f(-3+9+2)，
k?3＜-3+9+2，
得
------12分
------------１4分
20、解：（1）
為等差數列，∵
，又
，
∴ 
，
是方程
的兩個根
又公差
，∴
，∴
，
-------- 2分
∴ 
∴
∴
-----------4分
（2）由(1)知，
-----------5分
∴
∴
，
，
------------7分
∵
是等差數列，∴
，∴
----------8分
∴
（
舍去）
------------9分
（3）由(2)得
-------------11分
，
時取等號 ------- 13分
，
時取等號15分
(1)、(2)式中等號不可能同時取到，所以
-----------16分
21、解：（1）橢圓
與
相似. -----2分
因為的特征三角形是腰長為4，底邊長為
的等腰三角形，
而橢圓的特征三角形是腰長為2，
底邊長為
的等腰三角形，
因此兩個等腰三角形相似，且相似比為
.
---
6分
（2）橢圓
的方程為：
.
--------8分
假定存在，則設
、
所在直線為
，
中點為
.
則
.
-------10分
所以
.
中點在直線
上，所以有
. ----12分
.
. -------14分
（3）橢圓的方程為：.
兩個相似橢圓之間的性質有： 寫出一個給2分
① 兩個相似橢圓的面積之比為相似比的平方；
② 分別以兩個相似橢圓的頂點為頂點的四邊形也相似，相似比即為橢圓的相似比；
③ 兩個相似橢圓被同一條直線所截得的線段中點重合；
過原點的直線截相似橢圓所得線段長度之比恰為橢圓的相似比. ----20分
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com