
題目列表(包括答案和解析)
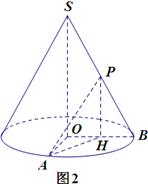
如圖,已知圓錐體 的側面積為
的側面積為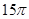 ,底面半徑
,底面半徑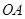 和
和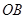 互相垂直,且
互相垂直,且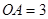 ,
, 是母線
是母線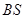 的中點.
的中點.

(1)求圓錐體的體積;
(2)異面直線 與
與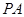 所成角的大小(結果用反三角函數表示).
所成角的大小(結果用反三角函數表示).
【解析】本試題主要考查了圓錐的體積和異面直線的所成的角的大小的求解。
第一問中,由題意, 得
得 ,故
,故
從而體積 .2中取OB中點H,聯結PH,AH.
.2中取OB中點H,聯結PH,AH.
由P是SB的中點知PH//SO,則 (或其補角)就是異面直線SO與PA所成角.
(或其補角)就是異面直線SO與PA所成角.
由SO 平面OAB,
平面OAB, PH
PH 平面OAB,PH
平面OAB,PH AH.在
AH.在 OAH中,由OA
OAH中,由OA OB得
OB得 ;
;
在 中,
中, ,PH=1/2SB=2,
,PH=1/2SB=2, ,
,
則 ,所以異面直線SO與P成角的大arctan
,所以異面直線SO與P成角的大arctan
解:(1)由題意, 得
得 ,
,
故 從而體積
從而體積 .
.
(2)如圖2,取OB中點H,聯結PH,AH.
由P是SB的中點知PH//SO,則 (或其補角)就是異面直線SO與PA所成角.
(或其補角)就是異面直線SO與PA所成角.
由SO 平面OAB,
平面OAB, PH
PH 平面OAB,PH
平面OAB,PH AH.
AH.
在 OAH中,由OA
OAH中,由OA OB得
OB得 ;
;
在 中,
中, ,PH=1/2SB=2,
,PH=1/2SB=2, ,
,
則 ,所以異面直線SO與P成角的大arctan
,所以異面直線SO與P成角的大arctan
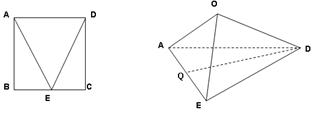
如圖,邊長為2的正方形ABCD,E是BC的中點,沿AE,DE將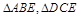 折起,使得B與C重合于O.
折起,使得B與C重合于O.
(Ⅰ)設Q為AE的中點,證明:QD AO;
AO;
(Ⅱ)求二面角O—AE—D的余弦值.
【解析】第一問中,利用線線垂直,得到線面垂直,然后利用性質定理得到線線垂直。取AO中點M,連接MQ,DM,由題意可得:AO EO, DO
EO, DO EO,
EO,
AO=DO=2.AO DM
DM
因為Q為AE的中點,所以MQ//E0,MQ AO
AO
AO 平面DMQ,AO
平面DMQ,AO DQ
DQ
第二問中,作MN AE,垂足為N,連接DN
AE,垂足為N,連接DN
因為AO EO, DO
EO, DO EO,EO
EO,EO 平面AOD,所以EO
平面AOD,所以EO DM
DM
,因為AO DM ,DM
DM ,DM 平面AOE
平面AOE
因為MN AE,DN
AE,DN AE,
AE,  DNM就是所求的DM=
DNM就是所求的DM= ,MN=
,MN=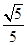 ,DN=
,DN= ,COS
,COS DNM=
DNM=
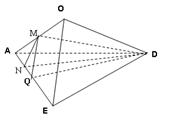
(1)取AO中點M,連接MQ,DM,由題意可得:AO EO, DO
EO, DO EO,
EO,
AO=DO=2.AO DM
DM
因為Q為AE的中點,所以MQ//E0,MQ AO
AO
AO 平面DMQ,AO
平面DMQ,AO DQ
DQ
(2)作MN AE,垂足為N,連接DN
AE,垂足為N,連接DN
因為AO EO, DO
EO, DO EO,EO
EO,EO 平面AOD,所以EO
平面AOD,所以EO DM
DM
,因為AO DM ,DM
DM ,DM 平面AOE
平面AOE
因為MN AE,DN
AE,DN AE,
AE,  DNM就是所求的DM=
DNM就是所求的DM= ,MN=
,MN=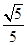 ,DN=
,DN= ,COS
,COS DNM=
DNM=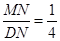
二面角O-AE-D的平面角的余弦值為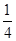
設數列 的各項均為正數.若對任意的
的各項均為正數.若對任意的 ,存在
,存在 ,使得
,使得 成立,則稱數列
成立,則稱數列 為“Jk型”數列.
為“Jk型”數列.
(1)若數列 是“J2型”數列,且
是“J2型”數列,且 ,
, ,求
,求 ;
;
(2)若數列 既是“J3型”數列,又是“J4型”數列,證明:數列
既是“J3型”數列,又是“J4型”數列,證明:數列 是等比數列.
是等比數列.
【解析】1)中由題意,得 ,
, ,
, ,
, ,…成等比數列,且公比
,…成等比數列,且公比 ,
,
所以.
(2)中證明:由{ }是“j4型”數列,得
}是“j4型”數列,得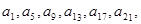 ,…成等比數列,設公比為t. 由{
,…成等比數列,設公比為t. 由{ }是“j3型”數列,得
}是“j3型”數列,得
 ,…成等比數列,設公比為
,…成等比數列,設公比為 ;
;
 ,…成等比數列,設公比為
,…成等比數列,設公比為 ;
;
 …成等比數列,設公比為
…成等比數列,設公比為 ;
;
已知m>1,直線 ,橢圓C:
,橢圓C: ,
, 、
、 分別為橢圓C的左、右焦點.
分別為橢圓C的左、右焦點.
(Ⅰ)當直線過右焦點 時,求直線的方程;
時,求直線的方程;
(Ⅱ)設直線與橢圓C交于A、B兩點,△A
 、△B
、△B
 的重心分別為G、H.若原點O在以線段GH為直徑的圓內,求實數m的取值范圍.[
的重心分別為G、H.若原點O在以線段GH為直徑的圓內,求實數m的取值范圍.[
【解析】第一問中因為直線 經過點
經過點 (
( ,0),所以
,0),所以 =
= ,得
,得 .又因為m>1,所以
.又因為m>1,所以 ,故直線的方程為
,故直線的方程為
第二問中設 ,由
,由 ,消去x,得
,消去x,得 ,
,
則由 ,知
,知 <8,且有
<8,且有
由題意知O為
 的中點.由
的中點.由 可知
可知 從而
從而 ,設M是GH的中點,則M(
,設M是GH的中點,則M( ).
).
由題意可知,2|MO|<|GH|,得到范圍
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com