
題目列表(包括答案和解析)
已知函數(shù) 的圖象過坐標(biāo)原點O,且在點
的圖象過坐標(biāo)原點O,且在點 處的切線的斜率是
處的切線的斜率是 .
.
(Ⅰ)求實數(shù) 的值;
的值;
(Ⅱ)求 在區(qū)間
在區(qū)間 上的最大值;
上的最大值;
(Ⅲ)對任意給定的正實數(shù) ,曲線
,曲線 上是否存在兩點P、Q,使得
上是否存在兩點P、Q,使得 是以O(shè)為直角頂點的直角三角形,且此三角形斜邊中點在
是以O(shè)為直角頂點的直角三角形,且此三角形斜邊中點在 軸上?說明理由.
軸上?說明理由.
【解析】第一問當(dāng) 時,
時, ,則
,則 。
。
依題意得: ,即
,即 解得
解得
第二問當(dāng) 時,
時, ,令
,令 得
得 ,結(jié)合導(dǎo)數(shù)和函數(shù)之間的關(guān)系得到單調(diào)性的判定,得到極值和最值
,結(jié)合導(dǎo)數(shù)和函數(shù)之間的關(guān)系得到單調(diào)性的判定,得到極值和最值
第三問假設(shè)曲線 上存在兩點P、Q滿足題設(shè)要求,則點P、Q只能在
上存在兩點P、Q滿足題設(shè)要求,則點P、Q只能在 軸兩側(cè)。
軸兩側(cè)。
不妨設(shè) ,則
,則 ,顯然
,顯然
∵ 是以O(shè)為直角頂點的直角三角形,∴
是以O(shè)為直角頂點的直角三角形,∴
即 (*)若方程(*)有解,存在滿足題設(shè)要求的兩點P、Q;
(*)若方程(*)有解,存在滿足題設(shè)要求的兩點P、Q;
若方程(*)無解,不存在滿足題設(shè)要求的兩點P、Q.
(Ⅰ)當(dāng) 時,
時, ,則
,則 。
。
依題意得: ,即
,即 解得
解得
(Ⅱ)由(Ⅰ)知,
①當(dāng) 時,
時, ,令
,令 得
得
當(dāng) 變化時,
變化時, 的變化情況如下表:
的變化情況如下表:
|
|
|
0 |
|
|
|
|
|
— |
0 |
+ |
0 |
— |
|
|
|
極小值 |
單調(diào)遞增 |
極大值 |
|
又 ,
, ,
, 。∴
。∴ 在
在 上的最大值為2.
上的最大值為2.
②當(dāng) 時,
時,  .當(dāng)
.當(dāng) 時,
時,  ,
, 最大值為0;
最大值為0;
當(dāng) 時,
時,  在
在 上單調(diào)遞增。∴
上單調(diào)遞增。∴ 在
在 最大值為
最大值為 。
。
綜上,當(dāng) 時,即
時,即 時,
時, 在區(qū)間
在區(qū)間 上的最大值為2;
上的最大值為2;
當(dāng) 時,即
時,即 時,
時, 在區(qū)間
在區(qū)間 上的最大值為
上的最大值為 。
。
(Ⅲ)假設(shè)曲線 上存在兩點P、Q滿足題設(shè)要求,則點P、Q只能在
上存在兩點P、Q滿足題設(shè)要求,則點P、Q只能在 軸兩側(cè)。
軸兩側(cè)。
不妨設(shè) ,則
,則 ,顯然
,顯然
∵ 是以O(shè)為直角頂點的直角三角形,∴
是以O(shè)為直角頂點的直角三角形,∴
即 (*)若方程(*)有解,存在滿足題設(shè)要求的兩點P、Q;
(*)若方程(*)有解,存在滿足題設(shè)要求的兩點P、Q;
若方程(*)無解,不存在滿足題設(shè)要求的兩點P、Q.
若 ,則
,則 代入(*)式得:
代入(*)式得:
即 ,而此方程無解,因此
,而此方程無解,因此 。此時
。此時 ,
,
代入(*)式得:  即
即 (**)
(**)
令
 ,則
,則
∴ 在
在 上單調(diào)遞增, ∵
上單調(diào)遞增, ∵  ∴
∴ ,∴
,∴ 的取值范圍是
的取值范圍是 。
。
∴對于 ,方程(**)總有解,即方程(*)總有解。
,方程(**)總有解,即方程(*)總有解。
因此,對任意給定的正實數(shù) ,曲線
,曲線 上存在兩點P、Q,使得
上存在兩點P、Q,使得 是以O(shè)為直角頂點的直角三角形,且此三角形斜邊中點在
是以O(shè)為直角頂點的直角三角形,且此三角形斜邊中點在 軸上
軸上
解:(Ⅰ)設(shè)![]() :
:![]()
![]() ,其半焦距為
,其半焦距為![]()
![]() .則
.則![]() :
:![]() .
.
由條件知![]() ,得
,得![]() .
.
![]() 的右準(zhǔn)線方程為
的右準(zhǔn)線方程為![]() ,即
,即![]() .
.
![]() 的準(zhǔn)線方程為
的準(zhǔn)線方程為![]() .
.
由條件知![]() , 所以
, 所以![]() ,故
,故![]() ,
,![]() .
.
從而![]() :
:![]() ,
, ![]() :
:![]() .
.
(Ⅱ)由題設(shè)知![]() :
:![]() ,設(shè)
,設(shè)![]() ,
,![]() ,
,![]() ,
,![]() .
.
由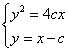 ,得
,得![]() ,所以
,所以![]() .
.
而![]() ,由條件
,由條件![]() ,得
,得![]() .
.
由(Ⅰ)得![]() ,
,![]() .從而,
.從而,![]() :
:![]() ,即
,即![]() .
.
由 ,得
,得![]() .所以
.所以![]() ,
,![]() .
.
故![]() .
.
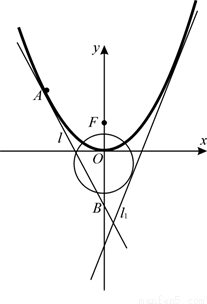
如圖,已知直線 (
(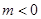 )與拋物線
)與拋物線 :
: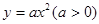 和圓
和圓 :
: 都相切,
都相切, 是
是 的焦點.
的焦點.
(Ⅰ)求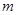 與
與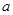 的值;
的值;
(Ⅱ)設(shè) 是
是 上的一動點,以
上的一動點,以 為切點作拋物線
為切點作拋物線 的切線
的切線 ,直線
,直線 交
交 軸于點
軸于點 ,以
,以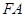 、
、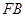 為鄰邊作平行四邊形
為鄰邊作平行四邊形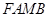 ,證明:點
,證明:點 在一條定直線上;
在一條定直線上;
(Ⅲ)在(Ⅱ)的條件下,記點 所在的定直線為
所在的定直線為 , 直線
, 直線 與
與 軸交點為
軸交點為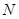 ,連接
,連接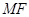 交拋物線
交拋物線 于
于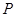 、
、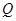 兩點,求△
兩點,求△ 的面積
的面積 的取值范圍.
的取值范圍.
【解析】第一問中利用圓 :
:
 的圓心為
的圓心為 ,半徑
,半徑 .由題設(shè)圓心到直線
.由題設(shè)圓心到直線 的距離
的距離 .
.
即 ,解得
,解得 (
( 舍去)
舍去)
設(shè) 與拋物線的相切點為
與拋物線的相切點為 ,又
,又 ,得
,得 ,
, .
.
代入直線方程得: ,∴
,∴ 所以
所以 ,
,
第二問中,由(Ⅰ)知拋物線 方程為
方程為 ,焦點
,焦點 . ………………(2分)
. ………………(2分)
設(shè) ,由(Ⅰ)知以
,由(Ⅰ)知以 為切點的切線
為切點的切線 的方程為
的方程為 .
.
令 ,得切線
,得切線 交
交 軸的
軸的 點坐標(biāo)為
點坐標(biāo)為 所以
所以 ,
, , ∵四邊形FAMB是以FA、FB為鄰邊作平行四邊形
, ∵四邊形FAMB是以FA、FB為鄰邊作平行四邊形
∴ 因為
因為 是定點,所以點
是定點,所以點 在定直線
在定直線
第三問中,設(shè)直線 ,代入
,代入 得
得 結(jié)合韋達(dá)定理得到。
結(jié)合韋達(dá)定理得到。
解:(Ⅰ)由已知,圓 :
:
 的圓心為
的圓心為 ,半徑
,半徑 .由題設(shè)圓心到直線
.由題設(shè)圓心到直線 的距離
的距離 .
.
即 ,解得
,解得 (
( 舍去). …………………(2分)
舍去). …………………(2分)
設(shè) 與拋物線的相切點為
與拋物線的相切點為 ,又
,又 ,得
,得 ,
, .
.
代入直線方程得: ,∴
,∴ 所以
所以 ,
, .
……(2分)
.
……(2分)
(Ⅱ)由(Ⅰ)知拋物線 方程為
方程為 ,焦點
,焦點 . ………………(2分)
. ………………(2分)
設(shè) ,由(Ⅰ)知以
,由(Ⅰ)知以 為切點的切線
為切點的切線 的方程為
的方程為 .
.
令 ,得切線
,得切線 交
交 軸的
軸的 點坐標(biāo)為
點坐標(biāo)為 所以
所以 ,
, , ∵四邊形FAMB是以FA、FB為鄰邊作平行四邊形,
, ∵四邊形FAMB是以FA、FB為鄰邊作平行四邊形,
∴ 因為
因為 是定點,所以點
是定點,所以點 在定直線
在定直線 上.…(2分)
上.…(2分)
(Ⅲ)設(shè)直線 ,代入
,代入 得
得 , ……)得
, ……)得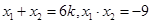 ,
…………………………… (2分)
,
…………………………… (2分)
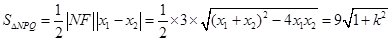 ,
,
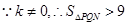 .
. △
△ 的面積
的面積 范圍是
范圍是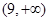
已知 ,設(shè)
,設(shè)
 和
和 是方程
是方程 的兩個根,不等式
的兩個根,不等式 對任意實數(shù)
對任意實數(shù) 恒成立;
恒成立; 函數(shù)
函數(shù) 有兩個不同的零點.求使“P且Q”為真命題的實數(shù)
有兩個不同的零點.求使“P且Q”為真命題的實數(shù) 的取值范圍.
的取值范圍.
【解析】本試題主要考查了命題和函數(shù)零點的運(yùn)用。由題設(shè)x1+x2=a,x1x2=-2,
∴|x1-x2|= =
= .
.
當(dāng)a∈[1,2]時, 的最小值為3. 當(dāng)a∈[1,2]時,
的最小值為3. 當(dāng)a∈[1,2]時, 的最小值為3.
的最小值為3.
要使|m-5|≤|x1-x2|對任意實數(shù)a∈[1,2]恒成立,只須|m-5|≤3,即2≤m≤8.
由已知,得f(x)=3x2+2mx+m+ =0的判別式
=0的判別式
Δ=4m2-12(m+ )=4m2-12m-16>0,
)=4m2-12m-16>0,
得m<-1或m>4.
可得到要使“P∧Q”為真命題,只需P真Q真即可。
解:由題設(shè)x1+x2=a,x1x2=-2,
∴|x1-x2|= =
= .
.
當(dāng)a∈[1,2]時, 的最小值為3.
的最小值為3.
要使|m-5|≤|x1-x2|對任意實數(shù)a∈[1,2]恒成立,只須|m-5|≤3,即2≤m≤8.
由已知,得f(x)=3x2+2mx+m+ =0的判別式
=0的判別式
Δ=4m2-12(m+ )=4m2-12m-16>0,
)=4m2-12m-16>0,
得m<-1或m>4.
綜上,要使“P∧Q”為真命題,只需P真Q真,即
解得實數(shù)m的取值范圍是(4,8]
如圖,在三棱錐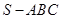 中,平面
中,平面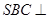 平面
平面 ,
,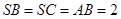 ,
,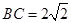 ,
,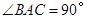 ,
,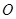 為
為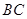 中點.(Ⅰ)求點B到平面
中點.(Ⅰ)求點B到平面 的距離;(Ⅱ)求二面角
的距離;(Ⅱ)求二面角 的余弦值.
的余弦值.

【解析】第一問中利用因為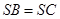 ,
,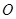 為
為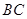 中點,所以
中點,所以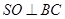
而平面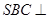 平面
平面 ,所以
,所以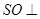 平面
平面 ,再由題設(shè)條件知道可以分別以
,再由題設(shè)條件知道可以分別以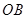 、
、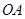 、
、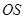 為
為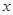 ,
,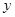 ,
,
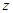 軸建立直角坐標(biāo)系得
軸建立直角坐標(biāo)系得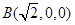 ,
,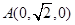 ,
,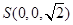 ,
,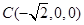 ,
,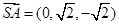 ,
,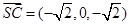 ,
,
故平面 的法向量
的法向量 而
而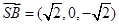 ,故點B到平面
,故點B到平面 的距離
的距離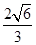
第二問中,由已知得平面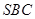 的法向量
的法向量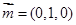 ,平面
,平面 的法向量
的法向量
故二面角 的余弦值等于
的余弦值等于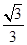
解:(Ⅰ)因為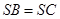 ,
,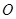 為
為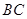 中點,所以
中點,所以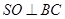
而平面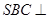 平面
平面 ,所以
,所以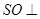 平面
平面 ,
,
再由題設(shè)條件知道可以分別以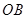 、
、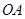 、
、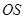 為
為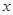 ,
,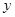 ,
,
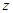 軸建立直角坐標(biāo)系,得
軸建立直角坐標(biāo)系,得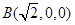 ,
,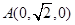 ,
,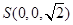 ,
,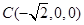 ,
,
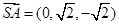 ,
,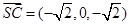 ,故平面
,故平面 的法向量
的法向量
而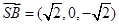 ,故點B到平面
,故點B到平面 的距離
的距離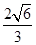
(Ⅱ)由已知得平面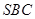 的法向量
的法向量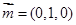 ,平面
,平面 的法向量
的法向量
故二面角 的余弦值等于
的余弦值等于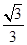
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com