
題目列表(包括答案和解析)
| 1 |
| 2 |
| AB |
| AC |
| 3 |
| 5 |
| 4 |
| 5 |
| 3 |
| 2 |
| 1 |
| 3 |
| π |
| 2 |
設(shè)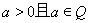 ,
,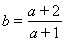 .
.
(Ⅰ)證明: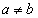 ;
;
(Ⅱ)求證:在數(shù)軸上,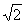 介于
介于 與
與 之間,且距
之間,且距 較遠(yuǎn);
較遠(yuǎn);
(Ⅲ)在數(shù)軸上, 之間的距離是否可能為整數(shù)?若有,則求出這個(gè)整數(shù);若沒有,
之間的距離是否可能為整數(shù)?若有,則求出這個(gè)整數(shù);若沒有,
說明理由.
設(shè) ,
, .
.
(Ⅰ)證明: ;
;
(Ⅱ)求證:在數(shù)軸上,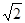 介于
介于 與
與 之間,且距
之間,且距 較遠(yuǎn);
較遠(yuǎn);
(Ⅲ)在數(shù)軸上,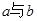 之間的距離是否可能為整數(shù)?若有,則求出這個(gè)整數(shù);若沒有,
之間的距離是否可能為整數(shù)?若有,則求出這個(gè)整數(shù);若沒有,
說明理由.
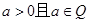 ,
, .
. ;
;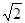 介于
介于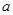 與
與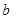 之間,且距
之間,且距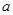 較遠(yuǎn);
較遠(yuǎn);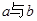 之間的距離是否可能為整數(shù)?若有,則求出這個(gè)整數(shù);若沒有,
之間的距離是否可能為整數(shù)?若有,則求出這個(gè)整數(shù);若沒有,一、選擇題:
1.D 2.A 3 B 4.D 5.A 6.D 7.B 8.C 9.A 10.B 11.A 12.B
二、填空題:
13.12 14.蒙古赤峰二中2009年3月高三統(tǒng)一考試--數(shù)學(xué)理科.files/image236.gif) 15 3 16.,①②③④
15 3 16.,①②③④
三、解答題:
17.解:法(1):①∵蒙古赤峰二中2009年3月高三統(tǒng)一考試--數(shù)學(xué)理科.files/image185.gif) =(1+cosB,sinB)與
=(1+cosB,sinB)與蒙古赤峰二中2009年3月高三統(tǒng)一考試--數(shù)學(xué)理科.files/image187.gif) =(0,1)所成的角為
=(0,1)所成的角為蒙古赤峰二中2009年3月高三統(tǒng)一考試--數(shù)學(xué)理科.files/image189.gif)
∴蒙古赤峰二中2009年3月高三統(tǒng)一考試--數(shù)學(xué)理科.files/image185.gif) 與向量
與向量蒙古赤峰二中2009年3月高三統(tǒng)一考試--數(shù)學(xué)理科.files/image239.gif) =(1,0)所成的角為
=(1,0)所成的角為蒙古赤峰二中2009年3月高三統(tǒng)一考試--數(shù)學(xué)理科.files/image241.gif)
∴蒙古赤峰二中2009年3月高三統(tǒng)一考試--數(shù)學(xué)理科.files/image243.gif) ,即
,即蒙古赤峰二中2009年3月高三統(tǒng)一考試--數(shù)學(xué)理科.files/image245.gif) (2分)
(2分)
而B∈(0,π),∴蒙古赤峰二中2009年3月高三統(tǒng)一考試--數(shù)學(xué)理科.files/image247.gif) ,∴
,∴蒙古赤峰二中2009年3月高三統(tǒng)一考試--數(shù)學(xué)理科.files/image249.gif) ,∴B=
,∴B=蒙古赤峰二中2009年3月高三統(tǒng)一考試--數(shù)學(xué)理科.files/image189.gif) 。 (4分)
。 (4分)
②令A(yù)B=c,BC=a,AC=b
∵B=蒙古赤峰二中2009年3月高三統(tǒng)一考試--數(shù)學(xué)理科.files/image189.gif) ,∴b2=a2+c2-2accosB=a2+c2-ac=
,∴b2=a2+c2-2accosB=a2+c2-ac=蒙古赤峰二中2009年3月高三統(tǒng)一考試--數(shù)學(xué)理科.files/image251.gif) ,∵a,c>0。
(6分)
,∵a,c>0。
(6分)
∴a2+c2≥蒙古赤峰二中2009年3月高三統(tǒng)一考試--數(shù)學(xué)理科.files/image253.gif) ,ac≤
,ac≤蒙古赤峰二中2009年3月高三統(tǒng)一考試--數(shù)學(xué)理科.files/image255.gif) (當(dāng)且僅當(dāng)a=c時(shí)等號(hào)成立)
(當(dāng)且僅當(dāng)a=c時(shí)等號(hào)成立)
∴12=a2+c2-ac≥蒙古赤峰二中2009年3月高三統(tǒng)一考試--數(shù)學(xué)理科.files/image257.gif)
蒙古赤峰二中2009年3月高三統(tǒng)一考試--數(shù)學(xué)理科.files/image259.gif) (8分)
(8分)
∴(a+c)2≤48,∴a+c≤蒙古赤峰二中2009年3月高三統(tǒng)一考試--數(shù)學(xué)理科.files/image261.gif) ,∴a+b+c≤
,∴a+b+c≤蒙古赤峰二中2009年3月高三統(tǒng)一考試--數(shù)學(xué)理科.files/image261.gif) +
+蒙古赤峰二中2009年3月高三統(tǒng)一考試--數(shù)學(xué)理科.files/image191.gif) =
=蒙古赤峰二中2009年3月高三統(tǒng)一考試--數(shù)學(xué)理科.files/image264.gif) (當(dāng)且僅當(dāng)a=c時(shí)取等號(hào))
(當(dāng)且僅當(dāng)a=c時(shí)取等號(hào))
故ΔABC的周長(zhǎng)的最大值為蒙古赤峰二中2009年3月高三統(tǒng)一考試--數(shù)學(xué)理科.files/image264.gif) 。 (10分)
。 (10分)
法2:(1)cos<蒙古赤峰二中2009年3月高三統(tǒng)一考試--數(shù)學(xué)理科.files/image185.gif) ,
,蒙古赤峰二中2009年3月高三統(tǒng)一考試--數(shù)學(xué)理科.files/image187.gif) >=cos
>=cos蒙古赤峰二中2009年3月高三統(tǒng)一考試--數(shù)學(xué)理科.files/image268.gif)
∴蒙古赤峰二中2009年3月高三統(tǒng)一考試--數(shù)學(xué)理科.files/image270.gif) , (2分)
, (2分)
即2cos2B+cosB-1=0,∴cosB=蒙古赤峰二中2009年3月高三統(tǒng)一考試--數(shù)學(xué)理科.files/image272.gif) 或cosB=-1(舍),而B∈(0,π),∴B=
或cosB=-1(舍),而B∈(0,π),∴B=蒙古赤峰二中2009年3月高三統(tǒng)一考試--數(shù)學(xué)理科.files/image189.gif) (4分)
(4分)
(2)令A(yù)B=c,BC=a,AC=b,ΔABC的周長(zhǎng)為蒙古赤峰二中2009年3月高三統(tǒng)一考試--數(shù)學(xué)理科.files/image275.gif) ,則
,則蒙古赤峰二中2009年3月高三統(tǒng)一考試--數(shù)學(xué)理科.files/image275.gif) =a+c+
=a+c+蒙古赤峰二中2009年3月高三統(tǒng)一考試--數(shù)學(xué)理科.files/image191.gif)
而a=b?蒙古赤峰二中2009年3月高三統(tǒng)一考試--數(shù)學(xué)理科.files/image278.gif) ,c=b?
,c=b?蒙古赤峰二中2009年3月高三統(tǒng)一考試--數(shù)學(xué)理科.files/image280.gif) (2分)
(2分)
∴蒙古赤峰二中2009年3月高三統(tǒng)一考試--數(shù)學(xué)理科.files/image275.gif) =
=蒙古赤峰二中2009年3月高三統(tǒng)一考試--數(shù)學(xué)理科.files/image282.gif) =
=蒙古赤峰二中2009年3月高三統(tǒng)一考試--數(shù)學(xué)理科.files/image284.gif)
=蒙古赤峰二中2009年3月高三統(tǒng)一考試--數(shù)學(xué)理科.files/image286.gif) (8分)
(8分)
∵A∈(0,蒙古赤峰二中2009年3月高三統(tǒng)一考試--數(shù)學(xué)理科.files/image288.gif) ),∴A-
),∴A-蒙古赤峰二中2009年3月高三統(tǒng)一考試--數(shù)學(xué)理科.files/image290.gif) ,
,
當(dāng)且僅當(dāng)A=蒙古赤峰二中2009年3月高三統(tǒng)一考試--數(shù)學(xué)理科.files/image189.gif) 時(shí),
時(shí),蒙古赤峰二中2009年3月高三統(tǒng)一考試--數(shù)學(xué)理科.files/image293.gif) 。
(10分)
。
(10分)
18.解法一:(1)∵PA⊥底面ABCD,BC蒙古赤峰二中2009年3月高三統(tǒng)一考試--數(shù)學(xué)理科.files/image295.gif) 平面AC,∴PA⊥BC
平面AC,∴PA⊥BC
∵∠ACB=90°,∴BC⊥AC,又PA∩AC=A,∴BC⊥平面PAC
(2)∵AB∥CD,∠BAD=120°,∴∠ADC=60°,又AD=CD=1
∴ΔADC為等邊三角形,且AC=1,取AC的中點(diǎn)O,則DO⊥AC,又PA⊥底面ABCD,
∴PA⊥DO,∴DO⊥平面PAC,過O作OH⊥PC,垂足為H,連DH
由三垂成定理知DH⊥PC,∴∠DHO為二面角D-PC-A的平面角
由OH=蒙古赤峰二中2009年3月高三統(tǒng)一考試--數(shù)學(xué)理科.files/image297.gif) ,DO=
,DO=蒙古赤峰二中2009年3月高三統(tǒng)一考試--數(shù)學(xué)理科.files/image299.gif) ,∴tan∠DHO=
,∴tan∠DHO=蒙古赤峰二中2009年3月高三統(tǒng)一考試--數(shù)學(xué)理科.files/image301.gif) =2
=2
∴二面角D-PC-A的大小的正切值為2。
蒙古赤峰二中2009年3月高三統(tǒng)一考試--數(shù)學(xué)理科.files/image302.gif) (3)設(shè)點(diǎn)B到平面PCD的距離為d,又AB∥平面PCD
(3)設(shè)點(diǎn)B到平面PCD的距離為d,又AB∥平面PCD
∴VA-PCD=VP-ACD,即蒙古赤峰二中2009年3月高三統(tǒng)一考試--數(shù)學(xué)理科.files/image304.gif)
∴蒙古赤峰二中2009年3月高三統(tǒng)一考試--數(shù)學(xué)理科.files/image306.gif) 即點(diǎn)B到平面PCD的距離為
即點(diǎn)B到平面PCD的距離為蒙古赤峰二中2009年3月高三統(tǒng)一考試--數(shù)學(xué)理科.files/image308.gif) 。
。
19.解:(1)第一和第三次取球?qū)Φ谒拇螣o影響,計(jì)第四次摸紅球?yàn)槭录嗀
①第二次摸紅球,則第四次摸球時(shí)袋中有4紅球概率為
蒙古赤峰二中2009年3月高三統(tǒng)一考試--數(shù)學(xué)理科.files/image310.gif) (2分)
(2分)
②第二次摸白球,則第四次摸球時(shí)袋中有5紅2白,摸紅球概率為
蒙古赤峰二中2009年3月高三統(tǒng)一考試--數(shù)學(xué)理科.files/image312.gif) (3分)
(3分)
∴P(A)=蒙古赤峰二中2009年3月高三統(tǒng)一考試--數(shù)學(xué)理科.files/image314.gif) ,即第四次恰好摸到紅球的概率為
,即第四次恰好摸到紅球的概率為蒙古赤峰二中2009年3月高三統(tǒng)一考試--數(shù)學(xué)理科.files/image316.gif) 。(6分)(注:無文字說明扣一分)
。(6分)(注:無文字說明扣一分)
(2)由題設(shè)可知ξ的所有可能取值為:ξ=0,1,2,3。P(ξ=0)=蒙古赤峰二中2009年3月高三統(tǒng)一考試--數(shù)學(xué)理科.files/image318.gif) ;
;
P(ξ=1)=蒙古赤峰二中2009年3月高三統(tǒng)一考試--數(shù)學(xué)理科.files/image320.gif) ;P(ξ=2)=
;P(ξ=2)=蒙古赤峰二中2009年3月高三統(tǒng)一考試--數(shù)學(xué)理科.files/image322.gif) ;
;
P(ξ=3)=蒙古赤峰二中2009年3月高三統(tǒng)一考試--數(shù)學(xué)理科.files/image324.gif) 。故隨機(jī)變量ξ的分布列為:
。故隨機(jī)變量ξ的分布列為:
ξ
0
1
2