
題目列表(包括答案和解析)
選修4-5:(本小題滿分10分)不等式選講
已知實(shí)數(shù)a、b、c、d滿足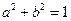 ,
,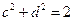 ,求ac+bd的最大值.
,求ac+bd的最大值.
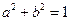 ,
,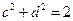 ,求ac+bd的最大值.
,求ac+bd的最大值. (選做題)本題包括A、B、C、D四小題,請(qǐng)選定其中兩題,并在答題卡指定區(qū)域內(nèi)作答,若多做,則按作答的前兩題評(píng)分,解答時(shí)應(yīng)寫出文字說明、證明過程或演算步驟.
(選做題)本題包括A、B、C、D四小題,請(qǐng)選定其中兩題,并在答題卡指定區(qū)域內(nèi)作答,若多做,則按作答的前兩題評(píng)分,解答時(shí)應(yīng)寫出文字說明、證明過程或演算步驟.
|
|
| 1 |
| 2a |
| 1 |
| 2b |
| 1 |
| 2c |
| 1 |
| b+c |
| 1 |
| c+a |
| 1 |
| a+b |
 (選做題)在A,B,C,D四小題中只能選做2題,每小題10分,共計(jì)20分.請(qǐng)?jiān)诖痤}卡指定區(qū)域內(nèi)作答,解答時(shí)應(yīng)寫出文字說明、證明過程或演算步驟.
(選做題)在A,B,C,D四小題中只能選做2題,每小題10分,共計(jì)20分.請(qǐng)?jiān)诖痤}卡指定區(qū)域內(nèi)作答,解答時(shí)應(yīng)寫出文字說明、證明過程或演算步驟.| 3 |
| 3 |
|
| 2 |
| π |
| 4 |
|
| 1 |
| 2a |
| 1 |
| 2b |
| 1 |
| 2c |
| 1 |
| b+c |
| 1 |
| c+a |
| 1 |
| a+b |
(選做題)本大題包括A,B,C,D共4小題,請(qǐng)從這4題中選做2小題. 每小題10分,共20分.請(qǐng)?jiān)诖痤}卡上準(zhǔn)確填涂題目標(biāo)記. 解答時(shí)應(yīng)寫出文字說明、證明過程或演算步驟.
A. 選修4-1:幾何證明選講
 如圖,
如圖, 是邊長為
是邊長為 的正方形,以
的正方形,以 為圓心,
為圓心, 為半徑的圓弧與以
為半徑的圓弧與以 為直徑的半⊙O交于點(diǎn)
為直徑的半⊙O交于點(diǎn) ,延長
,延長 交
交 于
于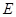 .
.
(1)求證: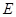 是
是 的中點(diǎn);(2)求線段
的中點(diǎn);(2)求線段 的長.
的長.
B.選修4-2:矩陣與變換
已知矩陣A ,其中
,其中 ,若點(diǎn)
,若點(diǎn) 在矩陣A的變換下得到
在矩陣A的變換下得到 .
.
(1)求實(shí)數(shù) 的值;
的值;
(2)矩陣A的特征值和特征向量.
C. 選修4-4:坐標(biāo)系與參數(shù)方程
在極坐標(biāo)系中,圓 的極坐標(biāo)方程為
的極坐標(biāo)方程為 ,
,
(1)過極點(diǎn)的一條直線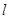 與圓相交于
與圓相交于 ,A兩點(diǎn),且∠
,A兩點(diǎn),且∠ ,求
,求 的長.
的長.
(2)求過圓上一點(diǎn) ,且與圓相切的直線的極坐標(biāo)方程;
,且與圓相切的直線的極坐標(biāo)方程;
D.選修4-5:不等式選講
已知實(shí)數(shù) 滿足
滿足 ,求
,求 的最小值;
的最小值;
8.1 9.0 10.學(xué).files/image233.gif) 11.
11.學(xué).files/image235.gif) 12.
12.學(xué).files/image237.gif) 13.
13.學(xué).files/image239.gif) 14.(1005,1004)
14.(1005,1004)
17.解:(1)依題意數(shù)列學(xué).files/image089.gif) 的通項(xiàng)公式是
的通項(xiàng)公式是學(xué).files/image326.gif) ,
,
知數(shù)列學(xué).files/image091.gif) 是首項(xiàng)為1,公比為2的等比數(shù)列。 ………6分
是首項(xiàng)為1,公比為2的等比數(shù)列。 ………6分
18.解:(Ⅰ)當(dāng)9天購買一次時(shí),該廠用于配料的保管費(fèi)用
(Ⅱ)(1)當(dāng)x≤7時(shí)
y=360x+10x+236=370x+236 ………5分
(2)當(dāng) x>7時(shí)
∴設(shè)該廠x天購買一次配料平均每天支付的費(fèi)用為f(x)元
當(dāng)x≤7時(shí)
當(dāng)x>7時(shí)
當(dāng)且僅當(dāng)x=12時(shí)取等號(hào)
∵393<404
∴當(dāng)x=12時(shí) f(x)有最小值393元 ………16分
(2)對(duì)于圓方程學(xué).files/image382.gif) ,令
,令學(xué).files/image384.gif) ,得
,得學(xué).files/image386.gif) ,即
,即學(xué).files/image388.gif) .又直線
.又直線學(xué).files/image390.gif) 過點(diǎn)
過點(diǎn)學(xué).files/image031.gif) 且與
且與學(xué).files/image099.gif) 軸垂直,∴直線
軸垂直,∴直線學(xué).files/image390.gif) 方程為
方程為學(xué).files/image395.gif) ,設(shè)
,設(shè)學(xué).files/image397.gif) ,則直線
,則直線學(xué).files/image399.gif) 方程為
方程為學(xué).files/image401.gif)
若圓學(xué).files/image411.gif) 經(jīng)過定點(diǎn),只需令
經(jīng)過定點(diǎn),只需令學(xué).files/image420.gif) ,從而有
,從而有學(xué).files/image422.gif) ,解得
,解得學(xué).files/image424.gif) ,
,
∴圓學(xué).files/image411.gif) 總經(jīng)過定點(diǎn)坐標(biāo)為
總經(jīng)過定點(diǎn)坐標(biāo)為學(xué).files/image426.gif) .
……………………… 14分
.
……………………… 14分
學(xué).files/image444.gif) 上存在唯一零點(diǎn),
上存在唯一零點(diǎn),學(xué).files/image446.gif) 上存在唯一的極值點(diǎn)………6分
上存在唯一的極值點(diǎn)………6分
取區(qū)間學(xué).files/image448.gif) 作為起始區(qū)間,用二分法逐次計(jì)算如下
作為起始區(qū)間,用二分法逐次計(jì)算如下
區(qū)間中點(diǎn)坐標(biāo)
中點(diǎn)對(duì)應(yīng)導(dǎo)數(shù)值
1
0.6
0.3
由上表可知區(qū)間學(xué).files/image465.gif) 的長度為0.3,所以該區(qū)間的中點(diǎn)
的長度為0.3,所以該區(qū)間的中點(diǎn)學(xué).files/image470.gif) ,到區(qū)間端點(diǎn)距離小于0.2,因此可作為誤差不超過0.2的一個(gè)極值點(diǎn)的相應(yīng)x的值。
,到區(qū)間端點(diǎn)距離小于0.2,因此可作為誤差不超過0.2的一個(gè)極值點(diǎn)的相應(yīng)x的值。
學(xué).files/image472.gif) 取得極值時(shí),相應(yīng)
取得極值時(shí),相應(yīng)學(xué).files/image474.gif) ………………………9分
………………………9分
數(shù)學(xué)附加題參考答案及評(píng)分標(biāo)準(zhǔn)
因?yàn)?sub>學(xué).files/image501.gif) ,所以∠ACD=∠ACB,AB=AD.
,所以∠ACD=∠ACB,AB=AD.
于是∠EAB=∠ACD. ……………………………………………4分
21B.解:設(shè)學(xué).files/image513.gif) 為曲線
為曲線學(xué).files/image515.gif) 上的任意一點(diǎn),在矩陣A變換下得到另一點(diǎn)
上的任意一點(diǎn),在矩陣A變換下得到另一點(diǎn)學(xué).files/image517.gif) ,
,
故有學(xué).files/image527.gif) 即所得曲線方程
即所得曲線方程學(xué).files/image529.gif) .………………………………………………… 10分
.………………………………………………… 10分
學(xué).files/image133.gif) 的極坐標(biāo)方程化為直角坐標(biāo)方程為
的極坐標(biāo)方程化為直角坐標(biāo)方程為學(xué).files/image532.gif) ,
,
即學(xué).files/image534.gif) ,它表示以
,它表示以學(xué).files/image536.gif) 為圓心,2為半徑的圓, ………………………………4分
為圓心,2為半徑的圓, ………………………………4分
圓C的圓心到直線l的距離學(xué).files/image541.gif) ,……………………………………………………………………8分
,……………………………………………………………………8分
故直線學(xué).files/image177.gif) 被曲線
被曲線學(xué).files/image133.gif) 截得的線段長度為
截得的線段長度為學(xué).files/image545.gif) . ……………………………………10分
. ……………………………………10分
學(xué).files/image557.gif) 22.以點(diǎn)
22.以點(diǎn)學(xué).files/image031.gif) 為坐標(biāo)原點(diǎn), 以
為坐標(biāo)原點(diǎn), 以學(xué).files/image560.gif) 分別為
分別為學(xué).files/image562.gif) 軸,建立如圖空間直角坐標(biāo)系, 不妨設(shè)
軸,建立如圖空間直角坐標(biāo)系, 不妨設(shè) 學(xué).files/image564.gif)
學(xué).files/image566.gif) 則
則
國際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com