
2009年高考數(shù)學(xué)難點突破專題輔導(dǎo)十一
難點11 函數(shù)中的綜合問題
函數(shù)綜合問題是歷年高考的熱點和重點內(nèi)容之一,一般難度較大,考查內(nèi)容和形式靈活多樣.本節(jié)課主要幫助考生在掌握有關(guān)函數(shù)知識的基礎(chǔ)上進一步深化綜合運用知識的能力,掌握基本解題技巧和方法,并培養(yǎng)考生的思維和創(chuàng)新能力.
●難點磁場
(★★★★★)設(shè)函數(shù)f(x)的定義域為R,對任意實數(shù)x、y都有f(x+y)=f(x)+f(y),當x>0時f(x)<0且f(3)=-4.
(1)求證:f(x)為奇函數(shù);
(2)在區(qū)間[-9,9]上,求f(x)的最值.
●案例探究
[例1]設(shè)f(x)是定義在R上的偶函數(shù),其圖象關(guān)于直線x=1對稱,對任意x1、x2∈[0, ],都有f(x1+x2)=f(x1)?f(x2),且f(1)=a>0.
],都有f(x1+x2)=f(x1)?f(x2),且f(1)=a>0.
(2)證明f(x)是周期函數(shù);
命題意圖:本題主要考查函數(shù)概念,圖象函數(shù)的奇偶性和周期性以及數(shù)列極限等知識,還考查運算能力和邏輯思維能力.
知識依托:認真分析處理好各知識的相互聯(lián)系,抓住條件f(x1+x2)=f(x1)?f(x2)找到問題的突破口.
錯解分析:不會利用f(x1+x2)=f(x1)?f(x2)進行合理變形.
技巧與方法:由f(x1+x2)=f(x1)?f(x2)變形為 是解決問題的關(guān)鍵.
是解決問題的關(guān)鍵.
(1)
解:因為對x1,x2∈[0, ],都有f(x1+x2)=f(x1)?f(x2),所以f(x)=
],都有f(x1+x2)=f(x1)?f(x2),所以f(x)= ≥0,
≥0,
x∈[0,1]
又f(1)=a>0
(2)證明:依題意設(shè)y=f(x)關(guān)于直線x=1對稱,故f(x)=f(1+1-x),即f(x)=f(2-x),x∈R.
又由f(x)是偶函數(shù)知f(-x)=f(x),x∈R
∴f(-x)=f(2-x),x∈R.
將上式中-x以x代換得f(x)=f(x+2),這表明f(x)是R上的周期函數(shù),且2是它的一個
周期.
(3)解:由(1)知f(x)≥0,x∈[0,1]
∵f( )=f(n?
)=f(n? )=f(
)=f( +(n-1)
+(n-1)  )=f(
)=f( )?f((n-1)?
)?f((n-1)? )
)
=……
又∵f(x)的一個周期是2
[例2]甲、乙兩地相距S千米,汽車從甲地勻速駛到乙地,速度不得超過c千米/小時,已知汽車每小時的運輸成本(以元為單位)由可變部分和固定部分組成,可變部分與速度v(km/h)的平方成正比,比例系數(shù)為b,固定部分為a元.
(1)把全程運輸成本y(元)表示為v(km/h)的函數(shù),并指出這個函數(shù)的定義域;
(2)為了使全程運輸成本最小,汽車應(yīng)以多大速度行駛?
命題意圖:本題考查建立函數(shù)的模型、不等式性質(zhì)、最值等知識,還考查學(xué)生綜合運用所學(xué)數(shù)學(xué)知識解決實際問題的能力.
知識依托:運用建模、函數(shù)、數(shù)形結(jié)合、分類討論等思想方法.
錯解分析:不會將實際問題抽象轉(zhuǎn)化為具體的函數(shù)問題,易忽略對參變量的限制條件.
技巧與方法:四步法:(1)讀題;(2)建模;(3)求解;(4)評價.
解法一:(1)依題意知,汽車從甲地勻速行駛到乙地所用時間為 ,全程運輸成本為y=a?
,全程運輸成本為y=a? +bv2?
+bv2? =S(
=S( +bv)
+bv)
∴所求函數(shù)及其定義域為y=S( +bv),v∈(0,c
+bv),v∈(0,c .
.
(2)依題意知,S、a、b、v均為正數(shù)
當且僅當 =bv,即v=
=bv,即v= 時,①式中等號成立.若
時,①式中等號成立.若 ≤c則當v=
≤c則當v= 時,有ymin;
時,有ymin;
∵c-v≥0,且c>bc2,∴a-bcv≥a-bc2>0
∴S( +bv)≥S(
+bv)≥S( +bc),當且僅當v=c時等號成立,也即當v=c時,有ymin;
+bc),當且僅當v=c時等號成立,也即當v=c時,有ymin;
綜上可知,為使全程運輸成本y最小,當 ≤c時,行駛速度應(yīng)為v=
≤c時,行駛速度應(yīng)為v= ,當
,當 >c時行駛速度應(yīng)為v=c.
>c時行駛速度應(yīng)為v=c.
解法二:(1)同解法一.
(2)∵函數(shù)y=x+ (k>0),x∈(0,+∞),當x∈(0,
(k>0),x∈(0,+∞),當x∈(0, )時,y單調(diào)減小,當x∈(
)時,y單調(diào)減小,當x∈( ,+∞)時y單調(diào)增加,當x=
,+∞)時y單調(diào)增加,當x= 時y取得最小值,而全程運輸成本函數(shù)為y=Sb(v+
時y取得最小值,而全程運輸成本函數(shù)為y=Sb(v+ ),v∈(0,c
),v∈(0,c .
.
∴當 ≤c時,則當v=
≤c時,則當v= 時,y最小,若
時,y最小,若 >c時,則當v=c時,y最小.結(jié)論同上.
>c時,則當v=c時,y最小.結(jié)論同上.
●錦囊妙計
在解決函數(shù)綜合問題時,要認真分析、處理好各種關(guān)系,把握問題的主線,運用相關(guān)的知識和方法逐步化歸為基本問題來解決,尤其是注意等價轉(zhuǎn)化、分類討論、數(shù)形結(jié)合等思想的綜合運用.綜合問題的求解往往需要應(yīng)用多種知識和技能.因此,必須全面掌握有關(guān)的函數(shù)知識,并且嚴謹審題,弄清題目的已知條件,尤其要挖掘題目中的隱含條件.
●殲滅難點訓(xùn)練
一、選擇題
1.(★★★★)函數(shù)y=x+a與y=logax的圖象可能是( )
2.(★★★★★)定義在區(qū)間(-∞,+∞)的奇函數(shù)f(x)為增函數(shù),偶函數(shù)g(x)在區(qū)間[0,+∞)的圖象與f(x)的圖象重合,設(shè)a>b>0,給出下列不等式:
①f(b)-f(-a)>g(a)-g(-b) ②f(b)-f(-a)<g(a)-g(-b) ③f(a)-f(-b)>g(b)-g(-a) ④f(a)-f(-b)<g(b)-g(-a)
其中成立的是( )
A.①與④ B.②與③ C.①與③ D.②與④
二、填空題
3.(★★★★)若關(guān)于x的方程22x+2xa+a+1=0有實根,則實數(shù)a的取值范圍是_________.
三、解答題
4.(★★★★)設(shè)a為實數(shù),函數(shù)f(x)=x2+|x-a|+1,x∈R.
(1)討論f(x)的奇偶性;
(2)求f(x)的最小值.
7.(★★★★★)某工廠擬建一座平面圖(如下圖)為矩形且面積為200平方米的三級污水處理池,由于地形限制,長、寬都不能超過

(1)寫出總造價y(元)與污水處理池長x(米)的函數(shù)關(guān)系式,并指出其定義域.
(2)求污水處理池的長和寬各為多少時,污水處理池的總造價最低?并求最低總造價.
8.(★★★★★)已知函數(shù)f(x)在(-∞,0)∪(0,+∞)上有定義,且在(0,+∞)上是增函數(shù),f(1)=0,又g(θ)=sin2θ-mcosθ-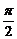 ],設(shè)M={m|g(θ)<0,m∈R},N={m|f[g(θ)]<0},求M∩N.
],設(shè)M={m|g(θ)<0,m∈R},N={m|f[g(θ)]<0},求M∩N.
[學(xué)法指導(dǎo)]怎樣學(xué)好函數(shù)
學(xué)習(xí)函數(shù)要重點解決好四個問題:準確深刻地理解函數(shù)的有關(guān)概念;揭示并認識函數(shù)與其他數(shù)學(xué)知識的內(nèi)在聯(lián)系;把握數(shù)形結(jié)合的特征和方法;認識函數(shù)思想的實質(zhì),強化應(yīng)用意識.
(一)準確、深刻理解函數(shù)的有關(guān)概念
概念是數(shù)學(xué)的基礎(chǔ),而函數(shù)是數(shù)學(xué)中最主要的概念之一,函數(shù)概念貫穿在中學(xué)代數(shù)的始終.數(shù)、式、方程、函數(shù)、排列組合、數(shù)列極限等是以函數(shù)為中心的代數(shù).近十年來,高考試題中始終貫穿著函數(shù)及其性質(zhì)這條主線.
(二)揭示并認識函數(shù)與其他數(shù)學(xué)知識的內(nèi)在聯(lián)系.函數(shù)是研究變量及相互聯(lián)系的數(shù)學(xué)概念,是變量數(shù)學(xué)的基礎(chǔ),利用函數(shù)觀點可以從較高的角度處理式、方程、不等式、數(shù)列、曲線與方程等內(nèi)容.在利用函數(shù)和方程的思想進行思維中,動與靜、變量與常量如此生動的辯證統(tǒng)一,函數(shù)思維實際上是辯證思維的一種特殊表現(xiàn)形式.
所謂函數(shù)觀點,實質(zhì)是將問題放到動態(tài)背景上去加以考慮.高考試題涉及5個方面:(1)原始意義上的函數(shù)問題;(2)方程、不等式作為函數(shù)性質(zhì)解決;(3)數(shù)列作為特殊的函數(shù)成為高考熱點;(4)輔助函數(shù)法;(5)集合與映射,作為基本語言和工具出現(xiàn)在試題中.
(三)把握數(shù)形結(jié)合的特征和方法
函數(shù)圖象的幾何特征與函數(shù)性質(zhì)的數(shù)量特征緊密結(jié)合,有效地揭示了各類函數(shù)和定義域、值域、單調(diào)性、奇偶性、周期性等基本屬性,體現(xiàn)了數(shù)形結(jié)合的特征與方法,為此,既要從定形、定性、定理、定位各方面精確地觀察圖形、繪制圖形,又要熟練地掌握函數(shù)圖象的平移變換、對稱變換.
(四)認識函數(shù)思想的實質(zhì),強化應(yīng)用意識
函數(shù)思想的實質(zhì)就是用聯(lián)系與變化的觀點提出數(shù)學(xué)對象,抽象數(shù)量特征,建立函數(shù)關(guān)系,求得問題的解決.縱觀近幾年高考題,考查函數(shù)思想方法尤其是應(yīng)用題力度加大,因此一定要認識函數(shù)思想實質(zhì),強化應(yīng)用意識.
難點磁場
(1)證明:令x=y=0,得f(0)=0
令y=-x,得f(0)=f(x)+f(-x),即f(-x)=-f(x)
∴f(x)是奇函數(shù)
(2)解:1°,任取實數(shù)x1、x2∈[-9,9]且x1<x2,這時,x2-x1>0,f(x1)-f(x2)=f[(x1-x2)+x2]-f(x2)=f(x1-x2)+f(x2)-f(x1)=-f(x2-x1)
因為x>0時f(x)<0,∴f(x1)-f(x2)>0
∴f(x)在[-9,9]上是減函數(shù)
故f(x)的最大值為f(-9),最小值為f(9).
而f(9)=f(3+3+3)=
∴f(x)在區(qū)間[-9,9]上的最大值為12,最小值為-12.
殲滅難點訓(xùn)練
一、1.解析:分類討論當a>1時和當0<a<1時.
答案:C
2.解析:用特值法,根據(jù)題意,可設(shè)f(x)=x,g(x)=|x|,又設(shè)a=2,b=1,
則f(a)=a,g(a)=|a|,f(b)=b,g(b)=|b|,f(a)-f(b)=f(2)-f(-1)=2+1=3.
g(b)-g(-a)=g(1)-g(-2)=1-2=-1.∴f(a)-f(-b)>g(1)-g(-2)=1-2=-1.
又f(b)-f(-a)=f(1)-f(-2)=1+2=3.
g(a)-g(-b)=g(2)-g(1)=2-1=1,∴f(b)-f(-a)=g(a)-g(-b).
即①與③成立.
答案:C
二、3.解析:設(shè)2x=t>0,則原方程可變?yōu)?i>t2+at+a+1=0 ①
三、4.解:(1)當a=0時,函數(shù)f(-x)=(-x)2+|-x|+1=f(x),此時f(x)為偶函數(shù);當a≠0時,f(a)=a2+1,f(-a)=a2+2|a|+1,f(-a)≠f(a),f(-a)≠-f(a).此時函數(shù)f(x)既不是奇函數(shù)也不是偶
函數(shù).
(2)①當x≤a時,函數(shù)f(x)=x2-x+a+1=(x- )2+a+
)2+a+ ,若a≤
,若a≤ ,則函數(shù)f(x)在(-∞,a
,則函數(shù)f(x)在(-∞,a 上單調(diào)遞減,從而,函數(shù)f(x)在(-∞,a
上單調(diào)遞減,從而,函數(shù)f(x)在(-∞,a 上的最小值為f(a)=a2+1.
上的最小值為f(a)=a2+1.
若a> ,則函數(shù)f(x)在(-∞,a
,則函數(shù)f(x)在(-∞,a 上的最小值為f(
上的最小值為f( )=
)= +a,且f(
+a,且f( )≤f(a).?
)≤f(a).?
②當x≥a時,函數(shù)f(x)=x2+x-a+1=(x+ )2-a+
)2-a+ ;當a≤-
;當a≤- 時,則函數(shù)f(x)在[a,+∞
時,則函數(shù)f(x)在[a,+∞ 上的最小值為f(-
上的最小值為f(- )=
)= -a,且f(-
-a,且f(- )≤f(a).若a>-
)≤f(a).若a>- ,?則函數(shù)f(x)在[a,+∞)上單調(diào)遞增,從而,函數(shù)f(x)在[a,+∞]上的最小值為f(a)=a2+1.
,?則函數(shù)f(x)在[a,+∞)上單調(diào)遞增,從而,函數(shù)f(x)在[a,+∞]上的最小值為f(a)=a2+1.
綜上,當a≤- 時,函數(shù)f(x)的最小值是
時,函數(shù)f(x)的最小值是 -a,當-
-a,當- <a≤
<a≤ 時,函數(shù)f(x)的最小值是a2+1;當a>
時,函數(shù)f(x)的最小值是a2+1;當a> 時,函數(shù)f(x)的最小值是a+
時,函數(shù)f(x)的最小值是a+ .
.
5.(1)證明:由 得f(x)的定義域為(-1,1),易判斷f(x)在(-1,1)內(nèi)是減函數(shù).
得f(x)的定義域為(-1,1),易判斷f(x)在(-1,1)內(nèi)是減函數(shù).
(2)證明:∵f(0)= ,∴f--1(
,∴f--1( )=0,即x=
)=0,即x= 是方程f--1(x)=0的一個解.若方程f--1(x)=0還有另一個解x0≠
是方程f--1(x)=0的一個解.若方程f--1(x)=0還有另一個解x0≠ ,則f--1(x0)=0,由反函數(shù)的定義知f(0)=x0≠
,則f--1(x0)=0,由反函數(shù)的定義知f(0)=x0≠ ,與已知矛盾,故方程f--1(x)=0有惟一解.
,與已知矛盾,故方程f--1(x)=0有惟一解.
(3)解:f[x(x- )]<
)]< ,即f[x(x-
,即f[x(x- )]<f(0).
)]<f(0).
6.證明:對f(x)+f(y)=f( )中的x,y,令x=y=0,得f(0)=0,再令y=-x,又得f(x)+f(-x)=f(0)=0,即f(-x)=-f(x),∴f(x)在x∈(-1,1)上是奇函數(shù).設(shè)-1<x1<x2<0,則f(x1)-f(x2)=f(x1)+f(-x2)=f(
)中的x,y,令x=y=0,得f(0)=0,再令y=-x,又得f(x)+f(-x)=f(0)=0,即f(-x)=-f(x),∴f(x)在x∈(-1,1)上是奇函數(shù).設(shè)-1<x1<x2<0,則f(x1)-f(x2)=f(x1)+f(-x2)=f( ),∵-1<x1<x2<0,∴x1-x2<0,1-x1x2>0.∴
),∵-1<x1<x2<0,∴x1-x2<0,1-x1x2>0.∴ <0,于是由②知f(
<0,于是由②知f( )?>0,從而f(x1)-f(x2)>0,即f(x1)>f(x2),故f(x)在x∈(-1,0)上是單調(diào)遞減函數(shù).根據(jù)奇函數(shù)的圖象關(guān)于原點對稱,知f(x)在x∈(0,1)上仍是遞減函數(shù),且f(x)<0.
)?>0,從而f(x1)-f(x2)>0,即f(x1)>f(x2),故f(x)在x∈(-1,0)上是單調(diào)遞減函數(shù).根據(jù)奇函數(shù)的圖象關(guān)于原點對稱,知f(x)在x∈(0,1)上仍是遞減函數(shù),且f(x)<0.
7.解:(1)因污水處理水池的長為x米,則寬為 米,總造價y=400(2x+2×
米,總造價y=400(2x+2× )+248×
)+248× ×2+80×200=800(x+
×2+80×200=800(x+ )+1600,由題設(shè)條件
)+1600,由題設(shè)條件
 解得12.5≤x≤16,即函數(shù)定義域為[12.5,16].
解得12.5≤x≤16,即函數(shù)定義域為[12.5,16].
(2)先研究函數(shù)y=f(x)=800(x+ )+16000在[12.5,16]上的單調(diào)性,對于任意的x1,x2∈[12.5,16],不妨設(shè)x1<x2,則f(x2)-f(x1)=800[(x2-x1)+324(
)+16000在[12.5,16]上的單調(diào)性,對于任意的x1,x2∈[12.5,16],不妨設(shè)x1<x2,則f(x2)-f(x1)=800[(x2-x1)+324( )]=800(x2-x1)(1-
)]=800(x2-x1)(1- ),∵12.5≤x1≤x2≤16.∴0<x1x2<162<324,∴
),∵12.5≤x1≤x2≤16.∴0<x1x2<162<324,∴ >1,即1-
>1,即1- <0.又x2-x1>0,∴f(x2)-f(x1)<0,即f(x2)<f(x1),故函數(shù)y=f(x)在[12.5,16]上是減函數(shù).∴當x=16時,y取得最小值,此時,ymin=800(16+
<0.又x2-x1>0,∴f(x2)-f(x1)<0,即f(x2)<f(x1),故函數(shù)y=f(x)在[12.5,16]上是減函數(shù).∴當x=16時,y取得最小值,此時,ymin=800(16+ )+16000=45000(元),
)+16000=45000(元), =12.5(米)?
=12.5(米)?
綜上,當污水處理池的長為
8.解:∵f(x)是奇函數(shù),且在(0,+∞)上是增函數(shù),∴f(x)在(-∞,0)上也是增函數(shù).
又f(1)=0,∴f(-1)=-f(1)=0,從而,當f(x)<0時,有x<-1或0<x<1,
則集合N={m|f[g(θ)]<θ= ={m|g(θ)<-1或0<g(θ)<1
={m|g(θ)<-1或0<g(θ)<1 ,
,
∴M∩N={m|g(θ)<-1 .由g(θ)<-1,得cos2θ>m(cosθ-2)+2,θ∈[0,
.由g(θ)<-1,得cos2θ>m(cosθ-2)+2,θ∈[0, ],令x=cosθ,x∈[0,1]得:x2>m(x-2)+2,x∈[0,1],令①:y1=x2,x∈[0,1]及②y2=m(m-2)+2,顯然①為拋物線一段,②是過(2,2)點的直線系,在同一坐標系內(nèi)由x∈[0,1]得y1>y2.∴m>4-2
],令x=cosθ,x∈[0,1]得:x2>m(x-2)+2,x∈[0,1],令①:y1=x2,x∈[0,1]及②y2=m(m-2)+2,顯然①為拋物線一段,②是過(2,2)點的直線系,在同一坐標系內(nèi)由x∈[0,1]得y1>y2.∴m>4-2 ,故M∩N={m|m>4-2
,故M∩N={m|m>4-2 }.
}.
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com