
科目: 來源: 題型:
【題目】在棱長為![]() 的正方體
的正方體![]() 中,
中,![]() 是面對角線
是面對角線![]() 上兩個不同的動點.以下四個命題:①存在
上兩個不同的動點.以下四個命題:①存在![]() 兩點,使
兩點,使![]() ;②存在
;②存在![]() 兩點,使
兩點,使![]() 與直線
與直線![]() 都成
都成![]() 的角;③若
的角;③若![]() ,則四面體
,則四面體![]() 的體積一定是定值;④若
的體積一定是定值;④若![]() ,則四面體
,則四面體![]() 在該正方體六個面上的正投影的面積的和為定值.其中為真命題的是____.
在該正方體六個面上的正投影的面積的和為定值.其中為真命題的是____.
查看答案和解析>>
科目: 來源: 題型:
【題目】已知直線![]() :
:![]() 與拋物線
與拋物線![]() 切于點
切于點![]() ,直線
,直線![]() :
:![]() 過定點Q,且拋物線
過定點Q,且拋物線![]() 上的點到點Q的距離與其到準線距離之和的最小值為
上的點到點Q的距離與其到準線距離之和的最小值為![]() .
.
(1)求拋物線![]() 的方程及點
的方程及點![]() 的坐標;
的坐標;
(2)設直線![]() 與拋物線
與拋物線![]() 交于(異于點P)兩個不同的點A、B,直線PA,PB的斜率分別為
交于(異于點P)兩個不同的點A、B,直線PA,PB的斜率分別為![]() ,那么是否存在實數
,那么是否存在實數![]() ,使得
,使得![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
查看答案和解析>>
科目: 來源: 題型:
【題目】團購已成為時下商家和顧客均非常青睞的一種省錢、高校的消費方式,不少商家同時加入多家團購網.現恰有三個團購網站在![]() 市開展了團購業務,
市開展了團購業務, ![]() 市某調查公司為調查這三家團購網站在本市的開展情況,從本市已加入了團購網站的商家中隨機地抽取了50家進行調查,他們加入這三家團購網站的情況如下圖所示.
市某調查公司為調查這三家團購網站在本市的開展情況,從本市已加入了團購網站的商家中隨機地抽取了50家進行調查,他們加入這三家團購網站的情況如下圖所示.
(1)從所調查的50家商家中任選兩家,求他們加入團購網站的數量不相等的概率;
(2)從所調查的50家商家中任取兩家,用![]() 表示這兩家商家參加的團購網站數量之差的絕對值,求隨機變量
表示這兩家商家參加的團購網站數量之差的絕對值,求隨機變量![]() 的分布列和數學期望;
的分布列和數學期望;
(3)將頻率視為概率,現從![]() 市隨機抽取3家已加入團購網站的商家,記其中恰好加入了兩個團購網站的商家數為
市隨機抽取3家已加入團購網站的商家,記其中恰好加入了兩個團購網站的商家數為![]() ,試求事件“
,試求事件“![]() ”的概率.
”的概率.

查看答案和解析>>
科目: 來源: 題型:
【題目】已知在直角坐標系![]() 中,曲線
中,曲線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數),以
為參數),以![]() 為極點,
為極點,![]() 軸正半軸為極軸建立極坐標系,曲線
軸正半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求曲線![]() 的普通方程與曲線
的普通方程與曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)曲線![]() 與曲線
與曲線![]() 有兩個公共點,求實數
有兩個公共點,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目: 來源: 題型:
【題目】共享單車是指由企業在校園、公交站點、商業區、公共服務區等場所提供的自行車單車共享服務,由于其依托“互聯網+”,符合“低碳出行”的理念,已越來越多地引起了人們的關注.某部門為了對該城市共享單車加強監管,隨機選取了50人就該城市共享單車的推行情況進行問卷調査,并將問卷中的這50人根據其滿意度評分值(百分制)按照![]() 分成5組,請根據下面尚未完成并有局部污損的頻率分布表和頻率分布直方圖(如圖所示)解決下列問題:
分成5組,請根據下面尚未完成并有局部污損的頻率分布表和頻率分布直方圖(如圖所示)解決下列問題:
頻率分布表
組別 | 分組 | 頻數 | 頻率 |
第1組 |
| 8 | 0.16 |
第2組 |
|
| ▆ |
第3組 |
| 20 | 0.40 |
第4組 |
| ▆ | 0.08 |
第5組 |
| 2 |
|
合計 | ▆ | ▆ |
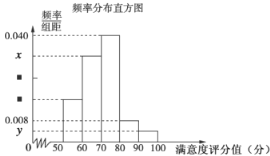
(1)求![]() 的值;
的值;
(2)若在滿意度評分值為![]() 的人中隨機抽取2人進行座談,求所抽取的2人中至少一人來自第5組的概率.
的人中隨機抽取2人進行座談,求所抽取的2人中至少一人來自第5組的概率.
查看答案和解析>>
科目: 來源: 題型:
【題目】為考察某動物疫苗預防某種疾病的效果,現對200只動物進行調研,并得到如下數據:
未發病 | 發病 | 合計 | |
未注射疫苗 | 20 | 60 | 80 |
注射疫苗 | 80 | 40 | 120 |
合計 | 100 | 100 | 200 |
(附: )
)
| 0.05 | 0.01 | 0.005 | 0.001 |
| 3.841 | 6.635 | 7.879 | 10.828 |
則下列說法正確的:( )
A.至少有99.9%的把握認為“發病與沒接種疫苗有關”
B.至多有99%的把握認為“發病與沒接種疫苗有關”
C.至多有99.9%的把握認為“發病與沒接種疫苗有關”
D.“發病與沒接種疫苗有關”的錯誤率至少有0.01%
查看答案和解析>>
科目: 來源: 題型:
【題目】在直角坐標系![]() 中,以原點
中,以原點![]() 為極點,
為極點,![]() 軸的正半軸為極軸建立極坐標系.若曲線
軸的正半軸為極軸建立極坐標系.若曲線![]() 的極坐標方程為
的極坐標方程為![]() ,
,![]() 點的極坐標為
點的極坐標為![]() ,在平面直角坐標系中直線
,在平面直角坐標系中直線![]() 經過點
經過點![]() ,且傾斜角為
,且傾斜角為![]() .
.
(1)寫出曲線![]() 的直角坐標方程以及點
的直角坐標方程以及點![]() 的直角坐標;
的直角坐標;
(2)設直線與曲線![]() 相交于
相交于![]() 、
、![]() 兩點,求
兩點,求![]() 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com