精品一区二区免费在线观看_国产精品久久久久久av福利软件_97成人精品区在线播放_国内成人精品一区

【題目】在平面直角坐標系中，為拋物線上不同的兩點，且，點且于點.

（1）求的值；

（2）過軸上一點 的直線交于，兩點，在的準線上的射影分別為，為的焦點，若，求中點的軌跡方程.

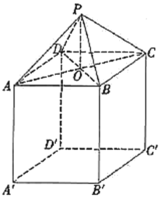
【題目】如圖所示，一個倉庫設計由上部屋頂和下部主體兩部分組成，屋頂的形狀是四棱錐，四邊形是正方形，點為正方形的中心，平面；下部的形狀是長方體.已知上部屋頂造價與屋頂面積成正比，比例系數為，下部主體造價與高度成正比，比例系數為.若欲造一個上、下總高度為10,的倉庫，則當總造價最低時，（ ）

A.B.C.4D.

【題目】在直角坐標系中,曲線的參數方程為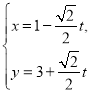(為參數).以坐標原點為極點,軸正半軸為極軸,建立極坐標系,曲線的極坐標方程為.

(1)寫出的普通方程及的直角坐標方程;

(2)設點在上,點在上,求的最小值及此時點的直角坐標.

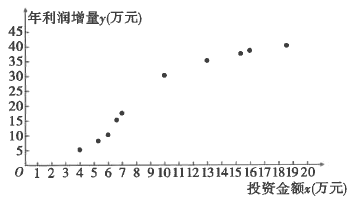
【題目】某果園種植“糖心蘋果”已有十余年,為了提高利潤,該果園每年投入一定的資金,對種植采摘包裝宣傳等環節進行改進.如圖是2009年至2018年,該果園每年的投資金額(單位:萬元)與年利潤增量(單位:萬元)的散點圖:

該果園為了預測2019年投資金額為20萬元時的年利潤增量,建立了關于的兩個回歸模型;

模型①:由最小二乘公式可求得與的線性回歸方程:;

模型②:由圖中樣本點的分布,可以認為樣本點集中在曲線:的附近,對投資金額做交換,令,則,且有,,,.

(1)根據所給的統計量,求模型②中關于的回歸方程;

(2)分別利用這兩個回歸模型,預測投資金額為20萬元時的年利潤增量(結果保留兩位小數);

(3)根據下列表格中的數據,比較兩種模型的相關指數,并說明誰的預測值精度更高更可靠.

附:樣本的最小乘估計公式為,;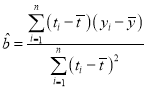

相關指數.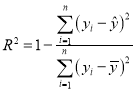

參考數據:,.

【題目】函數的定義域為,若存在一次函數,使得對于任意的,都有恒成立,則稱函數在上的弱漸進函數.下列結論正確的是__________.(寫出所有正確命題的序號)

①是在上的弱漸進函數;

②是在上的弱漸進函數;

③是在上的弱漸進函數;

④是在上的弱漸進函數.

【題目】在平面直角坐標系中，已知直線過點且傾斜角為，以坐標原點為極點，軸正半軸為極軸建立極坐標系，若曲線的極坐標方程為，且直線與曲線相交于,兩點.

（1）寫出曲線的直角坐標方程和直線的參數方程；

（2）若，求直線的直角坐標方程.

【題目】已知函數，其圖象的一條切線為.

（1）求實數的值；

（2）求證:若，則.

【題目】已知函數，，.

（1）求證:；

（2）若在上恒成立，求的最大值與的最小值.

【題目】如圖所示, 是邊長為3的正方形, 平面與平面所成角為.

(Ⅰ)求證： 平面；

(Ⅱ)設點是線段上一個動點,試確定點的位置,使得平面,并證明你的結論．

【題目】在平面直角坐標系xoy中，以坐標原點O為極點，x軸正半軸為極軸建立極坐標系。已知曲線C的極坐標方程為，過點的直線l的參數方程為（為參數），直線l與曲線C交于M、N兩點。

（1）寫出直線l的普通方程和曲線C的直角坐標方程：

（2）若成等比數列，求a的值。