
【題目】已知直線![]() 與曲線
與曲線![]() 和
和![]() 分別交于
分別交于![]() 兩點,點
兩點,點![]() 的坐標為
的坐標為![]() ,則
,則![]() 面積的最小值為( )
面積的最小值為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】C
【解析】
求出S△ABC![]() 2|BC|=et+t2﹣t+2,令f(t)=et+t2﹣t+2,t∈R,求出函數的導數,根據函數的單調性求出三角形面積的最小值即可.
2|BC|=et+t2﹣t+2,令f(t)=et+t2﹣t+2,t∈R,求出函數的導數,根據函數的單調性求出三角形面積的最小值即可.
由已知得B(t,et),C(t,﹣t2+t﹣2),
則|BC|=et+t2﹣t+2,
故S△ABC![]() 2|BC|=et+t2﹣t+2,
2|BC|=et+t2﹣t+2,
令f(t)=et+t2﹣t+2,t∈R,
f′(t)=et+2t﹣1,
f′(t)在R遞增,又f′(0)=0,
故t>0時,f′(t)>0,t<0時,f′(t)<0,
故f(t)在(﹣∞,0)遞減,在區間(0,+∞)遞增,
故f(t)min=e0+0﹣0+2=3,
故S△ABC的最小值是3,
故選:C.


 金鑰匙試卷系列答案
金鑰匙試卷系列答案科目:高中數學 來源: 題型:
【題目】某中學擬在高一下學期開設游泳選修課,為了了解高一學生喜歡游泳是否與性別有關,現從高一學生中抽取100人做調查,得到![]() 列聯表:
列聯表:
喜歡游泳 | 不喜歡游泳 | 合計 | |
男生 | 40 | ||
女生 | 30 | ||
合計 | 100 |
且已知在100個人中隨機抽取1人,抽到喜歡游泳的學生的概率為![]() .
.
(1)請完成上面的列聯表;
(2)根據列聯表的數據,是否有99.9%的把握認為喜歡游泳與性別有關?并說明你的理由.
參考公式與臨界值表:![]() .
.
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系xoy中,以坐標原點O為極點,x軸正半軸為極軸建立極坐標系。已知曲線C的極坐標方程為![]() ,過點
,過點![]() 的直線l的參數方程為
的直線l的參數方程為 (為參數),直線l與曲線C交于M、N兩點。
(為參數),直線l與曲線C交于M、N兩點。
(1)寫出直線l的普通方程和曲線C的直角坐標方程:
(2)若![]() 成等比數列,求a的值。
成等比數列,求a的值。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某地需要修建一條大型輸油管道通過720千米寬的荒漠地帶,該段輸油管道兩端的輸油站已建好,余下工程只需要在該段兩端已建好的輸油站之間鋪設輸油管道和等距離修建增壓站(又稱泵站).經預算,修建一個增壓站的工程費用為108萬元,鋪設距離為![]() 千米的相鄰兩增壓站之間的輸油管道費用為
千米的相鄰兩增壓站之間的輸油管道費用為![]() 萬元.設余下工程的總費用為
萬元.設余下工程的總費用為![]() 萬元.
萬元.
(1)試將![]() 表示成關于
表示成關于![]() 的函數;
的函數;
(2)需要修建多少個增壓站才能使總費用![]() 最小?
最小?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某企業為了增加某種產品的生產能力,提出甲、乙兩個方案。甲方案是廢除原有生產線并引進一條新生產線,需一次性投資1000萬元,年生產能力為300噸;乙方案是改造原有生產線,需一次性投資700萬元,年生產能力為200噸;根據市場調查與預測,該產品的年銷售量的頻率分布直方圖如圖所示,無論是引進新生產線還是改造原有生產線,設備的使用年限均為6年,該產品的銷售利潤為1.5萬元/噸。
(Ⅰ)根據年銷售量的頻率分布直方圖,估算年銷量的平均數![]() (同一組中的數據用該組區間的中點值作代表);
(同一組中的數據用該組區間的中點值作代表);
(Ⅱ)將年銷售量落入各組的頻率視為概率,各組的年銷售量用該組區間的中點值作年銷量的估計值,并假設每年的銷售量相互獨立。
(i)根據頻率分布直方圖估計年銷售利潤不低于270萬的概率;
(ii)以企業6年的凈利潤的期望值作為決策的依據,試判斷該企業應選擇哪個方案。(6年的凈利潤=6年銷售利潤-投資費用)

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一場小型晚會有![]() 個唱歌節目和
個唱歌節目和![]() 個相聲節目,要求排出一個節目單.
個相聲節目,要求排出一個節目單.
(1)![]() 個相聲節目要排在一起,有多少種排法?
個相聲節目要排在一起,有多少種排法?
(2)![]() 個相聲節目彼此要隔開,有多少種排法?
個相聲節目彼此要隔開,有多少種排法?
(3)第一個節目和最后一個節目都是唱歌節目,有多少種排法?
(4)前![]() 個節目中要有相聲節目,有多少種排法?
個節目中要有相聲節目,有多少種排法?
(要求:每小題都要有過程,且計算結果都用數字表示)
查看答案和解析>>
科目:高中數學 來源: 題型:
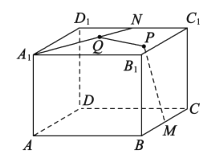
【題目】已知長方體![]() 中,底面ABCD的長AB=4,寬BC=4,高
中,底面ABCD的長AB=4,寬BC=4,高![]() =3,點M,N分別是BC,
=3,點M,N分別是BC,![]() 的中點,點P在上底面
的中點,點P在上底面![]() 中,點Q在
中,點Q在![]() 上,若
上,若![]() ,則PQ長度的最小值是
,則PQ長度的最小值是
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com