
【題目】已知函數(shù)![]() .
.
(Ⅰ)求曲線![]() 在點
在點![]() 處的切線方程;
處的切線方程;
(Ⅱ)證明:函數(shù)![]() 在區(qū)間
在區(qū)間![]() 上存在唯一的極大值點;
上存在唯一的極大值點;
(Ⅲ)證明:函數(shù)![]() 有且僅有一個零點.
有且僅有一個零點.
【答案】(Ⅰ)![]() (Ⅱ)證明見解析(Ⅲ)證明見解析
(Ⅱ)證明見解析(Ⅲ)證明見解析
【解析】
(Ⅰ)求導(dǎo),從而解得切線的切率,根據(jù)點斜式即可求得結(jié)果;
(Ⅱ)根據(jù)![]() 的單調(diào)性,即可容易求證;
的單調(diào)性,即可容易求證;
(Ⅲ)根據(jù)![]() 的正負,判斷函數(shù)
的正負,判斷函數(shù)![]() 的單調(diào)性,即可容易證明.
的單調(diào)性,即可容易證明.
(Ⅰ)因為![]() ,
,
所以![]() ,
,
![]() ,
,
又因為![]() ,
,
所以切線方程為![]() ,
,
即:![]() .
.
(Ⅱ)證明:因為![]() 和
和![]() 在
在![]() 上單調(diào)遞減,
上單調(diào)遞減,
所以![]() 在
在![]() 上單調(diào)遞減,
上單調(diào)遞減,
且![]() .
.
又![]() ,
,
所以在![]() 內(nèi)有且僅有一個實數(shù)
內(nèi)有且僅有一個實數(shù)![]() ,使得
,使得![]() =0,
=0,
并且當(dāng)![]() 時,
時,![]() ,
,
當(dāng)![]() 時,
時,![]() ,
,
所以![]() 在區(qū)間
在區(qū)間![]() 上有唯一的極大值點
上有唯一的極大值點![]() .
.
(Ⅲ)證明:當(dāng)![]() 時,
時,
![]() ,
,![]() ,
,
此時![]() .
.
當(dāng)![]() 時,
時,
![]() ,
,![]() ,
,
此時![]() .
.
當(dāng)![]() 時,
時,
因為![]() ,所以
,所以![]() 在
在![]() 內(nèi)單調(diào)遞增.
內(nèi)單調(diào)遞增.
因為![]() ,
,![]() ,
,
所以![]() 在
在![]() 上有且僅有一個零點.
上有且僅有一個零點.
綜上所述,函數(shù)![]() 有且僅有一個零點.
有且僅有一個零點.


 陽光課堂課時優(yōu)化作業(yè)系列答案
陽光課堂課時優(yōu)化作業(yè)系列答案科目:高中數(shù)學(xué) 來源: 題型:
【題目】隨著電商的快速發(fā)展,快遞業(yè)突飛猛進,到目前,中國擁有世界上最大的快遞市場.某快遞公司收取快遞費用的標(biāo)準(zhǔn)是:重量不超過![]() 的包裹收費10元;重量超過
的包裹收費10元;重量超過![]() 的包裹,除
的包裹,除![]() 收費10元之外,每超過
收費10元之外,每超過![]() (不足
(不足![]() ,按
,按![]() 計算)需再收5元.
計算)需再收5元.
該公司將最近承攬的100件包裹的重量統(tǒng)計如下:
包裹重量(單位: | 1 | 2 | 3 | 4 | 5 |
包裹件數(shù) | 43 | 30 | 15 | 8 | 4 |
公司對近60天,每天攬件數(shù)量統(tǒng)計如下表:
包裹件數(shù)范圍 | 0~100 | 101~200 | 201~300 | 301~400 | 401~500 |
包裹件數(shù)(近似處理) | 50 | 150 | 250 | 350 | 450 |
天數(shù) | 6 | 6 | 30 | 12 | 6 |
以上數(shù)據(jù)已做近似處理,并將頻率視為概率.
(1)計算該公司未來5天內(nèi)恰有2天攬件數(shù)在101~300之間的概率;
(2)①估計該公司對每件包裹收取的快遞費的平均值;
②根據(jù)以往的經(jīng)驗,公司將快遞費的三分之一作為前臺工作人員的工資和公司利潤,剩余的用作其他費用.目前前臺有工作人員3人,每人每件攬件不超過150件,日工資100元.公司正在考慮是否將前臺工作人員裁減1人,試計算裁員前后公司每日利潤的數(shù)學(xué)期望,若你是公司老總,是否進行裁減工作人員1人?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知![]() 為坐標(biāo)原點,點
為坐標(biāo)原點,點![]() ,
,![]() ,
,![]() ,動點
,動點![]() 滿足
滿足![]() ,點
,點![]() 為線段
為線段![]() 的中點,拋物線
的中點,拋物線![]() :
:![]() 上點
上點![]() 的縱坐標(biāo)為
的縱坐標(biāo)為![]() ,
,![]() .
.
(1)求動點![]() 的軌跡曲線
的軌跡曲線![]() 的標(biāo)準(zhǔn)方程及拋物線
的標(biāo)準(zhǔn)方程及拋物線![]() 的標(biāo)準(zhǔn)方程;
的標(biāo)準(zhǔn)方程;
(2)若拋物線![]() 的準(zhǔn)線上一點
的準(zhǔn)線上一點![]() 滿足
滿足![]() ,試判斷
,試判斷![]() 是否為定值,若是,求這個定值;若不是,請說明理由.
是否為定值,若是,求這個定值;若不是,請說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓![]() 的左右焦點分別為
的左右焦點分別為![]() ,
,![]() ,橢圓
,橢圓![]() 上一點
上一點![]() 到
到![]() 的距離之和為4.過點
的距離之和為4.過點![]() 作直線
作直線![]() 的垂線
的垂線![]() 交直線
交直線![]() 于點
于點![]() .
.
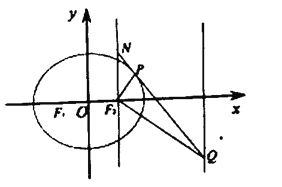
(1)求橢圓![]() 的標(biāo)準(zhǔn)方程;
的標(biāo)準(zhǔn)方程;
(2)試判斷直線![]() 與橢圓
與橢圓![]() 公共點的個數(shù),并說明理由;
公共點的個數(shù),并說明理由;
(3)直線![]() 與直線
與直線![]() 交于點
交于點![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】斜率為![]() 的直線
的直線![]() 過拋物線
過拋物線![]() 的焦點
的焦點![]() ,且與拋物線
,且與拋物線![]() 交于
交于![]() 、
、![]() 兩點.
兩點.
(1)設(shè)點![]() 在第一象限,過
在第一象限,過![]() 作拋物線
作拋物線![]() 的準(zhǔn)線的垂線,
的準(zhǔn)線的垂線,![]() 為垂足,且
為垂足,且![]() ,直線
,直線![]() 與直線
與直線![]() 關(guān)于直線
關(guān)于直線![]() 對稱,求直線
對稱,求直線![]() 的方程;
的方程;
(2)過![]() 且與
且與![]() 垂直的直線
垂直的直線![]() 與圓
與圓![]() 交于
交于![]() 、
、![]() 兩點,若
兩點,若![]() 與
與![]() 面積之和為
面積之和為![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() (其中
(其中![]() 為自然對數(shù)的底數(shù)).
為自然對數(shù)的底數(shù)).
(1)若![]() ,求函數(shù)
,求函數(shù)![]() 在區(qū)間
在區(qū)間![]() 上的最大值;
上的最大值;
(2)若![]() ,關(guān)于
,關(guān)于![]() 的方程
的方程![]() 有且僅有一個根, 求實數(shù)
有且僅有一個根, 求實數(shù)![]() 的取值范圍;
的取值范圍;
(3)若對任意![]() ,不等式
,不等式![]() 均成立, 求實數(shù)
均成立, 求實數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() 的圖象在
的圖象在![]() 處的切線為
處的切線為![]() .(
.(![]() 為自然對數(shù)的底數(shù)).
為自然對數(shù)的底數(shù)).
(1)求![]() ,
,![]() 的值;
的值;
(2)當(dāng)![]() 時,求證:
時,求證:![]() ;
;
(3)若![]() 對任意的
對任意的![]() 恒成立,求實數(shù)
恒成立,求實數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com