
【題目】如圖所示,已知多面體![]() 中,四邊形
中,四邊形![]() 為矩形,
為矩形, ![]() ,
, ![]() ,平面
,平面![]() 平面
平面![]() ,
, ![]() 、
、![]() 分別為
分別為![]() 、
、![]() 的中點.
的中點.
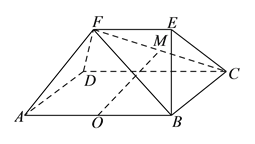
(![]() )求證:
)求證: ![]() .
.
(![]() )求證:
)求證: ![]() 平面
平面![]() .
.
(![]() )若過
)若過![]() 的平面交
的平面交![]() 于點
于點![]() ,交
,交![]() 于
于![]() ,求證:
,求證: ![]() .
.
【答案】(1)見解析;(2) 見解析(3)見解析
【解析】試題分析:
(1)由平面![]() 平面
平面![]() 可得
可得![]() 平面
平面![]() ,從而
,從而![]() 。又
。又![]() ,可得
,可得![]() 平面
平面![]() ,故得
,故得![]() .(2)取
.(2)取![]() 中點為
中點為![]() ,連接
,連接![]() ,
, ![]() ,可證得四邊形
,可證得四邊形![]() 是平行四邊形,故
是平行四邊形,故![]() ,由線面平行的判定定理可得
,由線面平行的判定定理可得![]() 平面
平面![]() .(3)由線面平行的性質及平行的傳遞性可得結論成立。
.(3)由線面平行的性質及平行的傳遞性可得結論成立。
試題解析:
(![]() )證明:∵ 平面
)證明:∵ 平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
, ![]() ,
,
∴ ![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,
,
∴ ![]() ,
,
又![]() ,
, ![]() ,
, ![]() 、
、![]() 平面
平面![]() ,
,
∴ ![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,
,
∴ ![]() .
.
(![]() )證明:取
)證明:取![]() 中點為
中點為![]() ,連接
,連接![]() ,
, ![]() ,
,
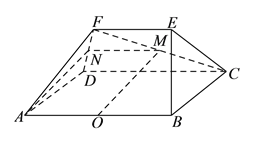
∵ ![]() 、
、![]() 分別為
分別為![]() ,
, ![]() 中點,
中點,
∴ ![]()
![]() ,
,
∴ ![]()
∴ 四邊形![]() 是平行四邊形,
是平行四邊形,
∴ ![]() ,
,
∴ ![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
∴ ![]() 平面
平面![]() .
.
(![]() )證明:∵
)證明:∵ ![]() ,
,
∴ 過直線![]() 存在一個平面
存在一個平面![]() ,使得平面
,使得平面![]() 平面
平面![]() ,
,
又過![]() 的平面交
的平面交![]() 于
于![]() 點,交
點,交![]() 于
于![]() 點,
點, ![]() 平面
平面![]() ,
,
∴ ![]() ,
,
∴ ![]() .
.


科目:高中數學 來源: 題型:
【題目】已知三棱錐S﹣ABC的各頂點都在一個半徑為r的球面上,且SA=SB=SC=1,AB=BC=AC=![]() ,則球的表面積為( )
,則球的表面積為( )
A. 12π B. 8π C. 4π D. 3π
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設數列{an}的前n項和為Sn=2n2,{bn}為等比數列,且a1=b1,b2(a2-a1)=b1.
(1)求數列{an}和{bn}的通項公式;
(2)設cn=![]() ,求數列{cn}的前n項和Tn.
,求數列{cn}的前n項和Tn.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() 是定義在
是定義在![]() 上的奇函數,且
上的奇函數,且![]() 為偶函數,對于函數
為偶函數,對于函數![]() 有下列幾種描述:
有下列幾種描述:
①![]() 是周期函數; ②
是周期函數; ②![]() 是它的一條對稱軸;
是它的一條對稱軸;
③![]() 是它圖象的一個對稱中心; ④當
是它圖象的一個對稱中心; ④當![]() 時,它一定取最大值;
時,它一定取最大值;
其中描述正確的是__________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系xOy中,以O為極點,x軸正半軸為極軸建立極坐標系,圓C的極坐標方程為ρ=2![]() cos
cos![]() ,直線l的參數方程為
,直線l的參數方程為![]() (t為參數),直線l與圓C交于A,B兩點,P是圓C上不同于A,B的任意一點.
(t為參數),直線l與圓C交于A,B兩點,P是圓C上不同于A,B的任意一點.
(1)求圓心的極坐標;
(2)求△PAB面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】有9本不同的課外書,分給甲、乙、丙三名同學,求在下列條件下,各有多少種分法?
(1)甲得4本,乙得3本,丙得2本;
(2)一人得4本,一人得3本,一人得2本;
(3)甲、乙、丙各得3本.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知由實數組成的等比數列{an}的前項和為Sn , 且滿足8a4=a7 , S7=254.
(1)求數列{an}的通項公式;
(2)對n∈N* , bn= ![]() ,求數列{bn}的前n項和Tn .
,求數列{bn}的前n項和Tn .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某投資人打算投資甲、乙兩個項目,根據預測,甲、乙項目可能的最大盈利率分別為100%和50%,可能的最大虧損率分別為30%和10%,投資人計劃投資金額不超過10萬元,要求確保可能的資金虧損不超過1.8萬元,問投資人對甲、乙兩個項目各投資多少萬元,才能使可能的盈利最大?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com