
【題目】已知函數(shù)![]() .
.
(1)若![]() ,曲線
,曲線![]() 在點
在點![]() 處的切線與直線
處的切線與直線![]() 平行,求
平行,求![]() 的值;
的值;
(2)若![]() ,且函數(shù)
,且函數(shù)![]() 的值域為
的值域為![]() ,求
,求![]() 的最小值.
的最小值.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)對函數(shù)進行求導(dǎo)得![]() ,再利用導(dǎo)數(shù)的幾何意義得
,再利用導(dǎo)數(shù)的幾何意義得![]() ,從而得到關(guān)于
,從而得到關(guān)于![]() 的方程,解方程即可得到答案;
的方程,解方程即可得到答案;
(2)當(dāng)![]() 時,
時,![]() ,將函數(shù)
,將函數(shù)![]() 可化為
可化為![]() ,則
,則![]() ,從而將問題轉(zhuǎn)化為
,從而將問題轉(zhuǎn)化為![]() 有解,再構(gòu)造函數(shù)
有解,再構(gòu)造函數(shù)![]() ,利用導(dǎo)數(shù)研究函數(shù)的值域,從而得到
,利用導(dǎo)數(shù)研究函數(shù)的值域,從而得到![]() 的取值范圍.
的取值范圍.
(1)當(dāng)![]() 時,
時,![]() ,
,
![]() ,
,
由![]() ,
,
得![]() ,
,
即![]() ,
,
解得![]() 或
或![]() ,
,
當(dāng)![]() 時,
時,![]() ,此時直線
,此時直線![]() 恰為切線,故舍去,
恰為切線,故舍去,
所以![]() .
.
(2)當(dāng)![]() 時,
時,![]() ,設(shè)
,設(shè)![]() ,
,
設(shè)![]() ,則
,則![]() ,
,
故函數(shù)![]() 可化為
可化為![]() .
.
由![]() ,可得
,可得
![]() 的單調(diào)遞減區(qū)間為
的單調(diào)遞減區(qū)間為![]() ,單調(diào)遞增區(qū)間為
,單調(diào)遞增區(qū)間為![]() ,
,
所以![]() 的最小值為
的最小值為![]() ,
,
此時![]() ,函數(shù)的
,函數(shù)的![]() 的值域為
的值域為![]()
問題轉(zhuǎn)化為當(dāng)![]() 時,
時,![]() 有解,
有解,
即![]() ,得
,得![]() .
.
設(shè)![]() ,則
,則![]() ,
,
故![]() 的單調(diào)遞減區(qū)間為
的單調(diào)遞減區(qū)間為![]() ,單調(diào)遞增區(qū)間為
,單調(diào)遞增區(qū)間為![]() ,
,
所以![]() 的最小值為
的最小值為![]() ,
,
故![]() 的最小值為
的最小值為![]() .
.


科目:高中數(shù)學(xué) 來源: 題型:
【題目】根據(jù)國家環(huán)保部新修訂的《 環(huán)境空氣質(zhì)量標(biāo)準(zhǔn)》規(guī)定:居民區(qū)![]() 的年平均濃度不得超過
的年平均濃度不得超過![]() 微克/立方米,
微克/立方米,![]() 的
的![]() 小時平均濃度不得超過
小時平均濃度不得超過![]() 微克/立方米.我市環(huán)保局隨機抽取了一居民區(qū)
微克/立方米.我市環(huán)保局隨機抽取了一居民區(qū)![]() 年
年![]() 天
天![]() 的
的![]() 小時平均濃度(單位:微克/立方米)的監(jiān)測數(shù)據(jù),數(shù)據(jù)統(tǒng)計如下表:
小時平均濃度(單位:微克/立方米)的監(jiān)測數(shù)據(jù),數(shù)據(jù)統(tǒng)計如下表:
組別 |
| 頻數(shù)(天) | 頻率 |
第一組 |
|
|
|
第二組 |
|
|
|
第三組 |
|
|
|
第四組 |
|
|
|
(1)這![]() 天的測量結(jié)果按上表中分組方法繪制成的樣本頻率分布直方圖如圖.
天的測量結(jié)果按上表中分組方法繪制成的樣本頻率分布直方圖如圖.

①求圖中![]() 的值;
的值;
②求樣本平均數(shù),并根據(jù)樣本估計總體的思想,從![]() 的年平均濃度考慮,判斷該居民區(qū)的環(huán)境質(zhì)量是否需要改善?并說明理由;
的年平均濃度考慮,判斷該居民區(qū)的環(huán)境質(zhì)量是否需要改善?并說明理由;
(2)將頻率視為概率,對于![]() 年的某
年的某![]() 天,記這
天,記這![]() 天中該居民區(qū)
天中該居民區(qū)![]() 的
的![]() 小時平均濃度符合環(huán)境空氣質(zhì)量標(biāo)準(zhǔn)的天數(shù)為
小時平均濃度符合環(huán)境空氣質(zhì)量標(biāo)準(zhǔn)的天數(shù)為![]() ,求
,求![]() 的分布列和數(shù)學(xué)期望.
的分布列和數(shù)學(xué)期望.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在四棱錐P﹣ABCD中,底面ABCD是邊長為2的菱形,∠DAB=60°,AD⊥PD,點F為棱PD的中點.
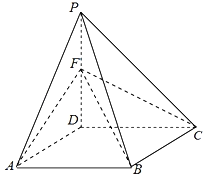
(1)在棱BC上是否存在一點E,使得CF∥平面PAE,并說明理由;
(2)若AC⊥PB,二面角D﹣FC﹣B的余弦值為![]() 時,求直線AF與平面BCF所成的角的正弦值.
時,求直線AF與平面BCF所成的角的正弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知正方體![]() ,過對角線
,過對角線![]() 作平面
作平面![]() 交棱
交棱![]() 于點
于點![]() ,交棱
,交棱![]() 于點
于點![]() ,下列正確的是( )
,下列正確的是( )
A.平面![]() 分正方體所得兩部分的體積相等;
分正方體所得兩部分的體積相等;
B.四邊形![]() 一定是平行四邊形;
一定是平行四邊形;
C.平面![]() 與平面
與平面![]() 不可能垂直;
不可能垂直;
D.四邊形![]() 的面積有最大值.
的面積有最大值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() .
.
(1)討論函數(shù)![]() 的單調(diào)性;
的單調(diào)性;
(2)若函數(shù)![]() 在區(qū)間
在區(qū)間![]() 上存在兩個不同零點,求實數(shù)
上存在兩個不同零點,求實數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知0<m<2,動點M到兩定點F1(﹣m,0),F2(m,0)的距離之和為4,設(shè)點M的軌跡為曲線C,若曲線C過點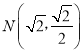 .
.
(1)求m的值以及曲線C的方程;
(2)過定點![]() 且斜率不為零的直線l與曲線C交于A,B兩點.證明:以AB為直徑的圓過曲線C的右頂點.
且斜率不為零的直線l與曲線C交于A,B兩點.證明:以AB為直徑的圓過曲線C的右頂點.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】政府工作報告指出,2019年我國深入實施創(chuàng)新驅(qū)動發(fā)展戰(zhàn)略,創(chuàng)新能力和效率進一步提升;2020年要提升科技支撐能力,健全以企業(yè)為主體的產(chǎn)學(xué)研一體化創(chuàng)新機制,某企業(yè)為了提升行業(yè)核心競爭力,逐漸加大了科技投入;該企業(yè)連續(xù)5年來的科技投入x(百萬元)與收益y(百萬元)的數(shù)據(jù)統(tǒng)計如下:
科技投入x | 1 | 2 | 3 | 4 | 5 |
收益y | 40 | 50 | 60 | 70 | 90 |
(1)請根據(jù)表中數(shù)據(jù),建立y關(guān)于x的線性回歸方程;
(2)按照(1)中模型,已知科技投入8百萬元時收益為140百萬元,求殘差![]() (殘差
(殘差![]() 真實值-預(yù)報值).
真實值-預(yù)報值).
參考數(shù)據(jù):回歸直線方程![]() ,其中
,其中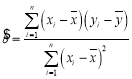 .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() .
.
![]() Ⅰ
Ⅰ![]() 若函數(shù)
若函數(shù)![]() 的最大值為3,求實數(shù)
的最大值為3,求實數(shù)![]() 的值;
的值;
![]() Ⅱ
Ⅱ![]() 若當(dāng)
若當(dāng)![]() 時,
時,![]() 恒成立,求實數(shù)
恒成立,求實數(shù)![]() 的取值范圍;
的取值范圍;
![]() Ⅲ
Ⅲ![]() 若
若![]() ,
,![]() 是函數(shù)
是函數(shù)![]() 的兩個零點,且
的兩個零點,且![]() ,求證:
,求證:![]() .
.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com