
設(shè)函數(shù) 定義在
定義在 上,對(duì)于任意實(shí)數(shù)
上,對(duì)于任意實(shí)數(shù)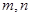 ,恒有
,恒有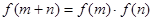 ,且當(dāng)
,且當(dāng)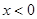 時(shí),
時(shí),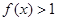
(1)求證: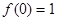 ,且當(dāng)
,且當(dāng)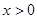 時(shí),
時(shí), 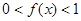
(2)求 在
在 上的單調(diào)性.
上的單調(diào)性.
(3)設(shè)集合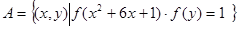 ,
,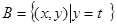 ,且
,且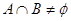 ,
,
求實(shí)數(shù)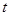 的取值范圍.
的取值范圍.
(1)見(jiàn)解析;(2) 在
在 上是減函數(shù). (3)
上是減函數(shù). (3)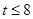 。
。
解析試題分析:(1)證明:取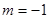 ,
,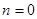 ,由已知
,由已知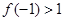
則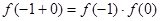 ,
,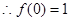 -----------2分
-----------2分
當(dāng)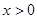 時(shí),
時(shí),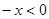 時(shí),則
時(shí),則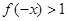
由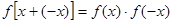 得
得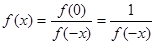
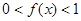 ----------4分
----------4分
(2)任取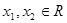 ,且
,且 .
.
則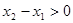
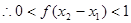 -----------5分
-----------5分 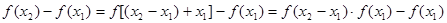
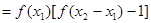 -----------6分
-----------6分 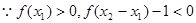
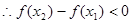 即
即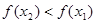
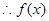 在
在 上是減函數(shù). -----------8分
上是減函數(shù). -----------8分
解(3)在集合 中,
中,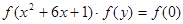
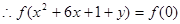
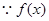 在
在 上是減函數(shù)
上是減函數(shù) 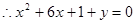 -------10分
-------10分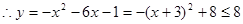
 ,
, 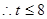 ---------12分
---------12分
考點(diǎn):抽象函數(shù)的性質(zhì)及應(yīng)用。
點(diǎn)評(píng):不給出具體解析式,只給出函數(shù)的特殊條件或特征的函數(shù)即為抽象函數(shù)。一般的:①求抽象函數(shù)的函數(shù)值常用賦值法。②證明抽象函數(shù)的單調(diào)性常用定義法。



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
某汽車生產(chǎn)企業(yè)上年度生產(chǎn)一品牌汽車的投入成本為10萬(wàn)元/輛,出廠價(jià)為13萬(wàn)元/輛,年銷售量為5000輛.本年度為適應(yīng)市場(chǎng)需求,計(jì)劃提高產(chǎn)品檔次,適當(dāng)增加投入成本,若每輛車投入成本增加的比例為 (0<
(0< <1
<1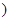 ,則出廠價(jià)相應(yīng)提高的比例為0.7
,則出廠價(jià)相應(yīng)提高的比例為0.7 ,年銷售量也相應(yīng)增加.已知年利潤(rùn)=(每輛車的出廠價(jià)-每輛車的投入成本)×年銷售量.
,年銷售量也相應(yīng)增加.已知年利潤(rùn)=(每輛車的出廠價(jià)-每輛車的投入成本)×年銷售量.
(1)若年銷售量增加的比例為0.4 ,為使本年度的年利潤(rùn)比上年度有所增加,則投入成本增加的比例
,為使本年度的年利潤(rùn)比上年度有所增加,則投入成本增加的比例 應(yīng)在什么范圍內(nèi)?
應(yīng)在什么范圍內(nèi)?
(2)年銷售量關(guān)于 的函數(shù)為
的函數(shù)為 ,則當(dāng)
,則當(dāng) 為何值時(shí),本年度的年利潤(rùn)最大?最大利潤(rùn)為多少?
為何值時(shí),本年度的年利潤(rùn)最大?最大利潤(rùn)為多少?
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
(本小題滿分12分)定義在實(shí)數(shù)R上的函數(shù)y= f(x)是偶函數(shù),當(dāng)x≥0時(shí),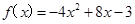 .
.
(Ⅰ)求f(x)在R上的表達(dá)式;
(Ⅱ)求y=f(x)的最大值,并寫出f(x)在R上的單調(diào)區(qū)間(不必證明).
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
(本題12分)
提高過(guò)立交橋的車輛通行能力可改善整個(gè)城市的交通狀況.在一般情況下,成都某立交橋上的車流速度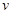 (單位:千米/小時(shí))是車流密度
(單位:千米/小時(shí))是車流密度 (單位:輛/千米)的函數(shù).當(dāng)橋上的車流密度達(dá)到200輛/千米時(shí),造成堵塞,此時(shí)車流速度為0;當(dāng)車流密度不超過(guò)20輛/千米時(shí),車流速度為60千米/小時(shí).研究表明:當(dāng)
(單位:輛/千米)的函數(shù).當(dāng)橋上的車流密度達(dá)到200輛/千米時(shí),造成堵塞,此時(shí)車流速度為0;當(dāng)車流密度不超過(guò)20輛/千米時(shí),車流速度為60千米/小時(shí).研究表明:當(dāng)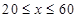 時(shí),車流速度
時(shí),車流速度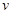 是車流密度
是車流密度 的一次函數(shù).
的一次函數(shù).
(Ⅰ)當(dāng)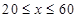 時(shí),求函數(shù)
時(shí),求函數(shù) 的表達(dá)式;
的表達(dá)式;
(Ⅱ)當(dāng)車流密度 為多大時(shí),車流量(單位時(shí)間內(nèi)通過(guò)橋上某觀測(cè)點(diǎn)的車輛數(shù),單位:輛/小時(shí))
為多大時(shí),車流量(單位時(shí)間內(nèi)通過(guò)橋上某觀測(cè)點(diǎn)的車輛數(shù),單位:輛/小時(shí))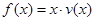 可以達(dá)到最大,并求出最大值.(精確到1輛/小時(shí))
可以達(dá)到最大,并求出最大值.(精確到1輛/小時(shí))
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
(本題滿分14分)建造一個(gè)容積為18立方米,深為2米的長(zhǎng)方體有蓋水池。如果池底和池壁每平方米的造價(jià)分別是200元和150元,那么如何建造,池的造價(jià)最低,為多少?
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
(本小題滿分14分)已知集合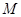 是滿足下列性質(zhì)的函數(shù)
是滿足下列性質(zhì)的函數(shù) 的全體:在定義域內(nèi)存在
的全體:在定義域內(nèi)存在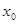 ,使得
,使得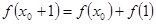 成立。
成立。
(Ⅰ)函數(shù)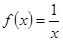 是否屬于集合
是否屬于集合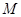 ?說(shuō)明理由;
?說(shuō)明理由;
(Ⅱ)設(shè)函數(shù) ,求
,求 的取值范圍;
的取值范圍;
(Ⅲ)設(shè)函數(shù) 圖象與函數(shù)
圖象與函數(shù)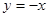 的圖象有交點(diǎn),
的圖象有交點(diǎn),
證明:函數(shù)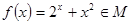 。
。
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
(本小題兩小題,每題6分,滿分12分)
⑴對(duì)任意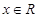 ,試比較
,試比較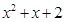 與
與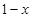 的大小;
的大小;
⑵已知函數(shù)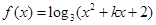 的定義域?yàn)镽,求實(shí)數(shù)k的取值范圍。
的定義域?yàn)镽,求實(shí)數(shù)k的取值范圍。
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
已知二次函數(shù)
(1)若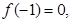 試判斷函數(shù)
試判斷函數(shù) 零點(diǎn)個(gè)數(shù);
零點(diǎn)個(gè)數(shù);
(2)若對(duì)任意的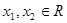 ,且
,且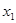 <
<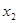 ,
,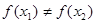 (
(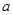 >0),試證明:
>0),試證明: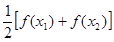 >
>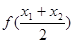 成立。
成立。
(3)是否存在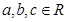 ,使
,使 同時(shí)滿足以下條件:①對(duì)任意
同時(shí)滿足以下條件:①對(duì)任意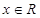 ,
, ,且
,且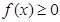 ②對(duì)任意的
②對(duì)任意的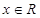 ,都有
,都有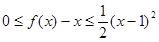 ?若存在,求出
?若存在,求出 的值,若不存在,請(qǐng)說(shuō)明理由。
的值,若不存在,請(qǐng)說(shuō)明理由。
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
(理科題)(本小題12分)
某房產(chǎn)開(kāi)發(fā)商投資81萬(wàn)元建一座寫字樓,第一年裝修費(fèi)為1萬(wàn)元,以后每年增加2萬(wàn)元,把寫字樓出租,每年收入租金30萬(wàn)元。
(1)若扣除投資和各種裝修費(fèi),則從第幾年開(kāi)始獲取純利潤(rùn)?
(2)若干年后開(kāi)發(fā)商為了投資其他項(xiàng)目,有兩種處理方案①年平均利潤(rùn)最大時(shí)以46萬(wàn)元出售該樓;
②純利潤(rùn)總和最大時(shí),以10萬(wàn)元出售樓,問(wèn)選擇哪種方案盈利更多?
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com