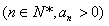的前n項和
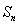滿足：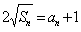
；設(shè)
，求數(shù)列
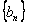的前n項和的最大值。 
寒假樂園北京教育出版社系列答案科目：高中數(shù)學(xué) 來源： 題型：
（12分）已知正項數(shù)列{
}的前n項和為
對任意
，
都有
。（Ⅰ）求數(shù)列的通項公式；
（Ⅱ）若
是遞增數(shù)列，求實數(shù)m的取值范圍。
查看答案和解析>>
科目：高中數(shù)學(xué) 來源：2014屆四川省高一下學(xué)期期中理科數(shù)學(xué)試卷（解析版） 題型：解答題
已知正項數(shù)列
的前n項和
滿足：
，
（1）求數(shù)列的通項
和前n項和；
（2）求數(shù)列
的前n項和
；
（3）證明：不等式 
對任意的
，
都成立．
【解析】第一問中，由于所以
兩式作差
，然后得到
從而
得到結(jié)論
第二問中，
利用裂項求和的思想得到結(jié)論。
第三問中，
又
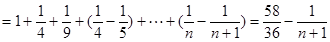
結(jié)合放縮法得到。
解：（1）∵ ∴
∴
∴
∴ ………2分
又∵正項數(shù)列，∴
∴
又n=1時，
∴
∴數(shù)列是以1為首項，2為公差的等差數(shù)列……………3分
∴
…………………4分
∴
…………………5分
（2）
…………………6分
∴
…………………9分
（3）
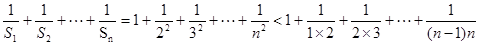
…………………12分
又
，
∴不等式 對任意的，都成立．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源：2011-2012學(xué)年新疆烏魯木齊市高三第三次月考理科數(shù)學(xué) 題型：解答題
（ 12分）已知正項數(shù)列
的前n項和滿足
（1）求數(shù)列的通項公式；
（2）設(shè)
是數(shù)列
的前n項的和，求證：
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
已知正項數(shù)列
的前n項和為
，且4，
成等比數(shù)列，向量a=(-1,1),b=(1,1),點
滿足
(1)求數(shù)列的通項公式。
（2）試判斷點
是否共線，并說明理由。
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
，所以
，即
，
；
時，由
，得
， ①
， ②
，
，
，
，
，
是以1為首項，以2為公差的等差數(shù)列，即
，
，
，
，
，
是等差數(shù)列，且
，公差d=-4，
，
時，
取最大值，但n∈N*，
最大，
。
