【題目】給出下列命題，其中錯誤命題的個數為( )
（1）直線
與平面
不平行，則與平面內的所有直線都不平行；
（2）直線與平面不垂直，則與平面內的所有直線都不垂直；
（3）異面直線、
不垂直，則過的任何平面與都不垂直；
（4）若直線和共面，直線和
共面，則和共面
A. 1 B. 2 C. 3 D. 4
勵耘書業暑假銜接寧波出版社系列答案科目：高中數學 來源： 題型：
【題目】平面四邊形
中， 
, 
為等邊三角形，現將
沿
翻折得到四面體
，點
分別為
的中點.
（Ⅰ）求證：四邊形
為矩形；
（Ⅱ）當平面
平面
時，求直線
與平面
所成角的正弦值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】交通安全法有規定：機動車行經人行橫道時，應當減速行駛；遇行人正在通過人行橫道，應當停車讓行.機動車行經沒有交通信號的道路時，遇行人橫過馬路，應當避讓.我們將符合這條規定的稱為“禮讓斑馬線”，不符合這條規定的稱為“不禮讓斑馬線”.下表是六安市某十字路口監控設備所抓拍的5個月內駕駛員“不禮讓斑馬線”行為的統計數據：
月份 | 1 | 2 | 3 | 4 | 5 |
“不禮讓斑馬線”的駕駛員人數 | 120 | 105 | 100 | 85 | 90 |
（1）根據表中所給的5個月的數據，可用線性回歸模型擬合
與
的關系，請用相關系數加以說明；
（2）求“不禮讓斑馬線”的駕駛員人數關于月份之間的線性回歸方程；
（3）若從4，5月份“不禮讓斑馬線”的駕駛員中分別選取4人和2人，再從所選取的6人中任意抽取2人進行交規調查，求抽取的2人分別來自兩個月份的概率；
參考公式：線性回歸方程
，其中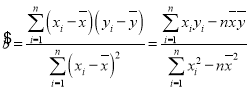
，
，
.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】下面四個命題：
①
在定義域上單調遞增；
②若銳角
，
滿足
，則
；
③
是定義在
上的偶函數，且在
上是增函數，若
，則
；
④函數
的一個對稱中心是
；
其中真命題的序號為______.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數
.
(1)當
時,求函數
的零點;
(2)當
,求函數
在
上的最大值;
(3)對于給定的正數a,有一個最大的正數
,使
時,都有
,試求出這個正數,并求它的取值范圍.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】十九大以來，某貧困地區扶貧辦積極貫徹落實國家精準扶貧的政策要求，帶領廣大農村地區人民群眾脫貧奔小康.經過不懈的奮力拼搏，新農村建設取得巨大進步，農民年收入也逐年增加.為了制定提升農民年收入、實現2020年脫貧的工作計劃，該地扶貧辦統計了2019年50位農民的年收入并制成如下頻率分布直方圖：
（1）根據頻率分布直方圖，估計50位農民的年平均收入
元（單位：千元）（同一組數據用該組數據區間的中點值表示）；
（2）由頻率分布直方圖，可以認為該貧困地區農民年收入X服從正態分布
，其中
近似為年平均收入，
近似為樣本方差
，經計算得
，利用該正態分布，求：
（i）在扶貧攻堅工作中，若使該地區約有占總農民人數的84.14%的農民的年收入高于扶貧辦制定的最低年收入標準，則最低年收入大約為多少千元？
（ii）為了調研“精準扶貧，不落一人”的政策要求落實情況，扶貧辦隨機走訪了1000位農民.若每位農民的年收入互相獨立，問：這1000位農民中的年收入不少于12.14千元的人數最有可能是多少？
附參考數據：
，若隨機變量X服從正態分布，則
，
，
.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】若函數
在
處取得極大值或極小值，則稱
為函數的極值點．設函數
，
，a，b，k
R．
（1）若
為
在x＝1處的切線．①當有兩個極值點
，
，且滿足·＝1時，求b的值及a的取值范圍；②當函數與的圖象只有一個交點，求a的值；
（2）若對滿足“函數與的圖象總有三個交點P，Q，R”的任意突數k，都有PQ＝QR成立，求a，b，k滿足的條件．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】從甲地到乙地要經過3個十字路口，設各路口信號燈工作相互獨立，且在各路口遇到紅燈的概率分別為
.
（Ⅰ）設
表示一輛車從甲地到乙地遇到紅燈的個數，求隨機變量
的分布列和數學期望；
（Ⅱ）若有2輛車獨立地從甲地到乙地，求這2輛車共遇到1個紅燈的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
