
【題目】已知拋物線![]() 的焦點為F,點
的焦點為F,點![]() 在此拋物線上,
在此拋物線上,![]() ,不過原點的直線
,不過原點的直線![]() 與拋物線C交于A,B兩點,以AB為直徑的圓M過坐標原點.
與拋物線C交于A,B兩點,以AB為直徑的圓M過坐標原點.
(1)求拋物線C的方程;
(2)證明:直線![]() 恒過定點;
恒過定點;
(3)若線段AB中點的縱坐標為2,求此時直線![]() 和圓M的方程.
和圓M的方程.
【答案】(1)![]() ;(2)定點
;(2)定點![]() ;(3)
;(3)![]() ,
,![]()
【解析】
(1)根據拋物線的定義,將![]() 轉化為拋物線上的點
轉化為拋物線上的點![]() 到準線的距離,從而求出
到準線的距離,從而求出![]() ,得到拋物線方程.
,得到拋物線方程.
(2)直線與拋物線聯立,得到![]() ,然后利用以
,然后利用以![]() 為直徑的圓
為直徑的圓![]() 過坐標原點,即
過坐標原點,即![]() ,代入
,代入![]() ,求出斜率與截距的關系,得到直線過的定點.
,求出斜率與截距的關系,得到直線過的定點.
(3)根據![]() 中點坐標,求出直線的斜率,得到直線方程,再求出
中點坐標,求出直線的斜率,得到直線方程,再求出![]() 長度,即圓的半徑,得到圓的方程.
長度,即圓的半徑,得到圓的方程.
(1)拋物線![]() ,其準線為
,其準線為![]()
![]() 點
點![]() 在此拋物線上,
在此拋物線上,![]() ,
,
![]() 點
點![]() 到準線的距離等于
到準線的距離等于![]() ,即
,即![]() ,得
,得![]()
![]() 所求拋物線方程為
所求拋物線方程為![]()
(2)①當直線![]() 斜率存在時,設直線
斜率存在時,設直線![]() 的方程為
的方程為![]() ,
,![]() ,易知
,易知![]() .
.
聯立方程組得![]() ,從而可得方程
,從而可得方程![]()
由題意可知![]()
![]()
所以![]()
因為以![]() 為直徑的圓
為直徑的圓![]() 過坐標原點,
過坐標原點,
所以![]() ,即
,即![]() ,所以
,所以![]() ,所以
,所以![]() .
.
所以直線![]() 的方程為
的方程為![]() ,即
,即![]() ,所以直線
,所以直線![]() 恒過定點
恒過定點![]() .
.
②當直線![]() 的斜率不存在時,易求得點
的斜率不存在時,易求得點![]() 坐標分別為
坐標分別為![]() ,
,![]() ,直線
,直線![]() 也過點
也過點![]() .
.
綜合①②可知,直線![]() 恒過定點
恒過定點![]() .
.
(3)由題意可知直線![]() 斜率存在,設線段
斜率存在,設線段![]() 中點坐標為
中點坐標為![]()
由(2)中所得![]() ,
,
則![]()
所以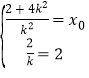 ,解得
,解得![]()
所以直線![]() 方程為
方程為![]() .
.
因為線段![]() 中點坐標為
中點坐標為![]() ,即為圓
,即為圓![]() 的圓心坐標,
的圓心坐標,
設圓![]()
![]() .
.
代入![]() ,得
,得![]()
所以圓![]() 的方程為
的方程為![]()


 輕松課堂單元期中期末專題沖刺100分系列答案
輕松課堂單元期中期末專題沖刺100分系列答案科目:高中數學 來源: 題型:
【題目】某小學為了解四年級學生的家庭作業用時情況,從本校四年級隨機抽取了一批學生進行調查,并繪制了學生作業用時的頻率分布直方圖,如圖所示.
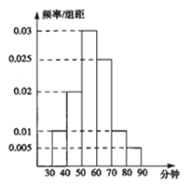
(1)估算這批學生的作業平均用時情況;
(2)作業用時不能完全反映學生學業負擔情況,這與學生自身的學習習慣有很大關系如果用時四十分鐘之內評價為優異,一個小時以上為一般,其它評價為良好.現從優異和良好的學生里面用分層抽樣的方法抽取300人,其中女生有90人(優異20人).請完成列聯表,并根據列聯表分析能否在犯錯誤的概率不超過0.05的前提下認為學習習慣與性別有關系?
男生 | 女生 | 合計 | |
良好 | |||
優異 | |||
合計 |
附:![]() ,其中
,其中![]()
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】微信是騰訊公司推出的一種手機通訊軟件,它支持發送語音短信、視頻、圖片和文字,一經推出便風靡全國,甚至涌現出一批在微信的朋友圈內銷售商品的人(被稱為微商).為了調查每天微信用戶使用微信的時間,某經銷化妝品的微商在一廣場隨機采訪男性、女性用戶各![]() 名,將男性、女性使用微信的時間分成
名,將男性、女性使用微信的時間分成![]() 組:
組:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分別加以統計,得到如圖所示的頻率分布直方圖.
分別加以統計,得到如圖所示的頻率分布直方圖.

(1)根據女性頻率分布直方圖,估計女性使用微信的平均時間;
(2)若每天玩微信超過![]() 小時的用戶列為“微信控”,否則稱其為“非微信控”,請你根據已知條件完成
小時的用戶列為“微信控”,否則稱其為“非微信控”,請你根據已知條件完成![]() 的列聯表,并判斷是否有
的列聯表,并判斷是否有![]() 的把握認為“微信控”與“性別”有關?
的把握認為“微信控”與“性別”有關?
參考公式:![]() ,其中
,其中![]() .
.
參考數據:

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】新聞出版業不斷推進供給側結構性改革,深入推動優化升級和融合發展,持續提高優質出口產品供給,實現了行業的良性發展.下面是2012年至2016年我國新聞出版業和數字出版業營收增長情況,則下列說法錯誤的是( )
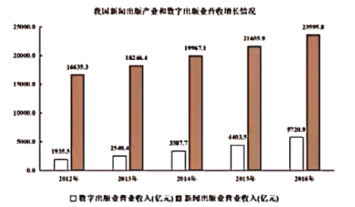
A. 2012年至2016年我國新聞出版業和數字出版業營收均逐年增加
B. 2016年我國數字出版業營收超過2012年我國數字出版業營收的2倍
C. 2016年我國新聞出版業營收超過2012年我國新聞出版業營收的1.5倍
D. 2016年我國數字出版營收占新聞出版營收的比例未超過三分之一
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設拋物線![]() 的焦點為
的焦點為![]() ,過點
,過點![]() 作直線
作直線![]() 與拋物線交于
與拋物線交于![]() ,
,![]() 兩點,點
兩點,點![]() 滿足
滿足![]() ,過
,過![]() 作
作![]() 軸的垂線與拋物線交于點
軸的垂線與拋物線交于點![]() ,若
,若![]() ,則點
,則點![]() 的橫坐標為__________,
的橫坐標為__________,![]() __________.
__________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的兩個焦點與短軸的一個端點是等邊三角形的三個頂點,且長軸長為4
的兩個焦點與短軸的一個端點是等邊三角形的三個頂點,且長軸長為4
(1)求橢圓![]() 的方程;
的方程;
(2)若![]() 是橢圓
是橢圓![]() 的左頂點,經過左焦點
的左頂點,經過左焦點![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 交于
交于![]() 、
、![]() 兩點,求
兩點,求![]() 與
與![]() 的面積之差的絕對值的最大值,并求取得最大值時直線
的面積之差的絕對值的最大值,并求取得最大值時直線![]() 的方程.
的方程.![]() 為坐標原點)
為坐標原點)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設橢圓![]() 的右焦點為
的右焦點為![]() ,右頂點為
,右頂點為![]() .已知
.已知![]() ,其中
,其中![]() 為原點,
為原點, ![]() 為橢圓的離心率.
為橢圓的離心率.
(1)求橢圓的方程及離心率![]() 的值;
的值;
(2)設過點![]() 的直線
的直線![]() 與橢圓交于點
與橢圓交于點![]() (
(![]() 不在
不在![]() 軸上),垂直于
軸上),垂直于![]() 的直線與
的直線與![]() 交于點
交于點![]() ,與
,與![]() 軸交于點
軸交于點![]() .若
.若![]() ,且
,且![]() ,求直線
,求直線![]() 的斜率的取值范圍.
的斜率的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,
中,![]() ,底面ABCD是邊長為3的正方形,EFG分別是棱ABPBPC的中點,
,底面ABCD是邊長為3的正方形,EFG分別是棱ABPBPC的中點,![]() ,
,![]() .
.

(Ⅰ)求證:平面EFG∥平面PAD;
(Ⅱ)求三棱錐![]() 的體積.
的體積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com