【題目】如圖所示，某游樂園的一個摩天輪半徑為10米，輪子的底部在地面上2米處，如果此摩天輪每20分鐘轉一圈，當摩天輪上某人經過
處時開始計時（按逆時針方向轉），
（其中
平行于地面）.
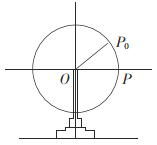
（1）求開始轉動5分鐘時此人相對于地面的高度.
（2）開始轉動
分鐘時，摩天輪上此人經過點
，求
的值.
【答案】（1）
（米）；（2）10
【解析】
（1）根據題意以
為坐標原點，以
所在直線為
軸建立平面直角坐標系，可求得在
分鐘時此人相對于地面高度的解析式，代入
即可求解.
（2）由題意可知轉動
分鐘時轉過的角度，即可求得
的坐標；根據題意可求得
的坐標，由兩點間距離公式即可求得
的值.
（1）以為坐標原點，以所在直線為軸建立平面直角坐標系，如下圖所示：
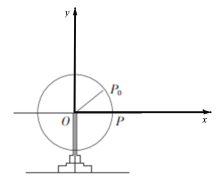
設摩天輪上某人所在的點為
，則在分鐘內
轉過的角為
，
摩天輪半徑為10米，輪子的底部在地面上2米處，
所以分鐘時，點的縱坐標為
，
所以在分鐘時此人相對于地面的高度為
，
所以5分鐘后的高度為
（米）.
（2）由（1）可知，在分鐘內轉過的角為
，
，
由題意可知
，
由
可求得
，
則由兩點間距離公式可得
.
科目：高中數學 來源： 題型：
【題目】已知函數f（x）＝（k＋
）lnx＋
，k∈[4，＋∞），曲線y＝f（x）上總存在兩點M（x1，y1），N（x2，y2），使曲線y＝f（x）在M，N兩點處的切線互相平行，則x1＋x2的取值范圍為
A. （
，＋∞） B. （
，＋∞） C. [，＋∞） D. [，＋∞）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數
，
，
.
（1）當
時，若對任意
均有
成立，求實數
的取值范圍；
（2）設直線
與曲線
和曲線
相切，切點分別為
，
，其中
.
①求證：
；
②當
時，關于
的不等式
恒成立，求實數
的取值范圍.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】海水養殖場進行某水產品的新、舊網箱養殖方法的產量對比，收獲時各隨機抽取了100個網箱，測量各箱水產品的產量（單位：kg）, 其頻率分布直方圖如下：
（1）記A表示事件“舊養殖法的箱產量低于50 kg”，估計A的概率；
（2）填寫下面列聯表，并根據列聯表判斷是否有99%的把握認為箱產量與養殖方法有關：
箱產量＜50 kg | 箱產量≥50 kg | |
舊養殖法 | ||
新養殖法 |
（3）根據箱產量的頻率分布直方圖，對這兩種養殖方法的優劣進行比較.
附：
P（ | 0.050 0.010 0.001 |
k | 3.841 6.635 10.828 |
. 
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】為了解甲、乙兩個快遞公司的工作狀況，假設同一個公司快遞員的工作狀況基本相同，現從甲、乙兩公司各隨機抽取一名快遞員，并從兩人某月（30天）的快遞件數記錄結果中隨機抽取10天的數據，制表如圖：
每名快遞員完成一件貨物投遞可獲得的勞務費情況如下：甲公司規定每件4.5元；乙公司規定每天35件以內（含35件）的部分每件4元，超出35件的部分每件7元.
（1）根據表中數據寫出甲公司員工A在這10天投遞的快遞件數的平均數和眾數；
（2）為了解乙公司員工B的每天所得勞務費的情況，從這10天中隨機抽取1天，他所得的勞務費記為X（單位：元），求X的分布列和數學期望；
（3）根據表中數據估算兩公司的每位員工在該月所得的勞務費.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】給定橢圓
，稱圓心在原點
，半徑為
的圓是橢圓
的“準圓”.若橢圓
的一個焦點為
，其短軸上的一個端點到
的距離為
.
（1）求橢圓
的方程和其“準圓”方程；
（2）點
是橢圓
的“準圓”上的動點，過點
作橢圓的切線
交“準圓”于點
.
①當點
為“準圓”與
軸正半軸的交點時，求直線
的方程并證明
；
②求證：線段
的長為定值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，四邊形
是邊長為2的正方形．
平面
，且
．
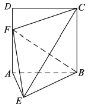
（1）求證：平面
平面
．
（2）線段
上是否存在一點
，使三棱錐
的高
若存在，請求出
的值；若不存在，請說明理由．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
