
【題目】已知函數![]() 與
與![]() 的圖象關于直線
的圖象關于直線![]() 對稱. (
對稱. (![]() 為自然對數的底數)
為自然對數的底數)
(1)若![]() 的圖象在點
的圖象在點![]() 處的切線經過點
處的切線經過點![]() ,求
,求![]() 的值;
的值;
(2)若不等式![]() 恒成立,求正整數
恒成立,求正整數![]() 的最小值.
的最小值.
【答案】(1)e;(2)2.
【解析】
(1)根據反函數的性質,得出![]() ,再利用導數的幾何意義,求出曲線
,再利用導數的幾何意義,求出曲線![]() 在點
在點![]() 處的切線為
處的切線為![]() ,構造函數
,構造函數![]() ,利用導數求出單調性,即可得出
,利用導數求出單調性,即可得出![]() 的值;
的值;
(2)設![]() ,求導
,求導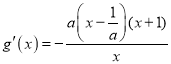 ,求出
,求出![]() 的單調性,從而得出最大值為
的單調性,從而得出最大值為![]() ,結合恒成立的性質,得出正整數
,結合恒成立的性質,得出正整數![]() 的最小值.
的最小值.
(1)根據題意,![]() 與
與![]() 的圖象關于直線
的圖象關于直線![]() 對稱,
對稱,
所以函數![]() 的圖象與
的圖象與![]() 互為反函數,則
互為反函數,則![]() ,,
,,
設點![]() ,
,![]() ,又
,又![]() ,
,
當![]() 時,
時,![]() ,
,
曲線![]() 在點
在點![]() 處的切線為
處的切線為![]() ,
,
即![]() ,代入點
,代入點![]() ,
,
得![]() ,即
,即![]() ,
,
構造函數![]() ,
,
當![]() 時,
時,![]() ,
,
當![]() 時,
時,![]() ,
,
且![]() ,當
,當![]() 時,
時,![]() 單調遞增,
單調遞增,
而![]() , 故
, 故![]() 存在唯一的實數根
存在唯一的實數根![]() .
.
(2)由于不等式![]() 恒成立,
恒成立,
可設![]() ,
,
所以![]()
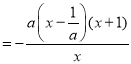 ,
,
令![]() ,得
,得![]() .
.
所以當![]() 時,
時,![]() ;當
;當![]() 時,
時,![]() ,
,
因此函數![]() 在
在![]() 是增函數,在
是增函數,在![]()
![]() 是減函數.
是減函數.
故函數![]() 的最大值為
的最大值為![]()
![]() .
.
令![]() ,
,
因為![]() ,
,![]()
![]() ,
,
又因為![]() 在
在![]() 是減函數.
是減函數.
所以當![]() 時,
時,![]() .
.
所以正整數![]() 的最小值為2.
的最小值為2.


科目:高中數學 來源: 題型:
【題目】已知a>0,b>0,則“1![]() 2”是“a2+a=3b2+2b”的( )
2”是“a2+a=3b2+2b”的( )
A.充分不必要條件B.必要不充分條件
C.充分必要條件D.既不充分也不必要條件
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】隨著經濟模式的改變,微商和電商已成為當今城鄉一種新型的購銷平臺.已知經銷某種商品的電商在任何一個銷售季度內,沒售出1噸該商品可獲利潤0.5萬元,未售出的商品,每1噸虧損0.3萬元.根據往年的銷售經驗,得到一個銷售季度內市場需求量的頻率分布直方圖如圖所示.已知電商為下一個銷售季度籌備了130噸該商品,現以![]() (單位:噸,
(單位:噸,![]() )表示下一個銷售季度的市場需求量,
)表示下一個銷售季度的市場需求量,![]() (單位:萬元)表示該電商下一個銷售季度內經銷該商品獲得的利潤.
(單位:萬元)表示該電商下一個銷售季度內經銷該商品獲得的利潤.
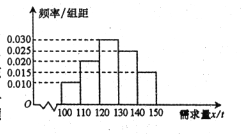
(Ⅰ)視![]() 分布在各區間內的頻率為相應的概率,求
分布在各區間內的頻率為相應的概率,求![]() ;
;
(Ⅱ)將![]() 表示為
表示為![]() 的函數,求出該函數表達式;
的函數,求出該函數表達式;
(Ⅲ)在頻率分布直方圖的市場需求量分組中,以各組的區間中點值(組中值)代表該組的各個值,并以市場需求量落入該區間的頻率作為市場需求量取該組中值的概率(例如![]() ,則取
,則取![]() 的概率等于市場需求量落入
的概率等于市場需求量落入![]() 的頻率),求
的頻率),求![]() 的分布列及數學期望
的分布列及數學期望![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某貧困地區幾個丘陵的外圍有兩條相互垂直的直線型公路![]() ,
,![]() ,以及鐵路線上的一條應開鑿的直線穿山隧道
,以及鐵路線上的一條應開鑿的直線穿山隧道![]() ,為進一步改善山區的交通現狀,計劃修建一條連接兩條公路
,為進一步改善山區的交通現狀,計劃修建一條連接兩條公路![]() ,
,![]() 和山區邊界的直線型公路
和山區邊界的直線型公路![]() ,以
,以![]() ,
,![]() 所在的直線分別為
所在的直線分別為![]() 軸,
軸,![]() 軸,建立平面直角坐標系
軸,建立平面直角坐標系![]() ,如圖所示,山區邊界曲線為
,如圖所示,山區邊界曲線為![]() :
:![]() ,設公路
,設公路![]() 與曲線
與曲線![]() 相切于點
相切于點![]() .
.
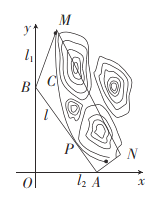
(1)設公路![]() 交
交![]() 軸,
軸,![]() 軸分別為
軸分別為![]() ,
,![]() 兩點,若公路
兩點,若公路![]() 的斜率為-1,求
的斜率為-1,求![]() 的長;
的長;
(2)在(1)條件下,測得四邊形![]() 中,
中,![]() ,
,![]() ,
,![]() 千米,
千米,![]() 千米,求應開鑿的隧道
千米,求應開鑿的隧道![]() 的長度.
的長度.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知在等比數列{an}中,![]() =2,,
=2,,![]() =128,數列{bn}滿足b1=1,b2=2,且{
=128,數列{bn}滿足b1=1,b2=2,且{![]() }為等差數列.
}為等差數列.
(1)求數列{an}和{bn}的通項公式;
(2)求數列{bn}的前n項和.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,曲線
中,曲線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數),以坐標原點為極點,
為參數),以坐標原點為極點,![]() 軸正半軸為極軸建立極坐標系.直線
軸正半軸為極軸建立極坐標系.直線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求曲線![]() 的極坐標方程與直線
的極坐標方程與直線![]() 的直角坐標方程;
的直角坐標方程;
(2)已知直線![]() 與曲線
與曲線![]() 交于
交于![]() 兩點,與
兩點,與![]() 軸交于點
軸交于點![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知常數a≠0,數列![]() 的前n項和為
的前n項和為![]() ,且
,且![]()
(1)求證:數列![]() 為等差數列;
為等差數列;
(2)若![]() 且數列
且數列![]() 是單調遞增數列,求實數a的取值范圍;
是單調遞增數列,求實數a的取值范圍;
(3)若![]() 數列
數列![]() 滿足:
滿足: ![]() 對于任意給定的正整數k,是否存在p,
對于任意給定的正整數k,是否存在p,![]() ,使
,使![]() 若存在,求p,q的值(只要寫出一組即可);若不存在,說明理由.
若存在,求p,q的值(只要寫出一組即可);若不存在,說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com