
【題目】已知函數![]() .
.
(1)若曲線![]() 的切線方程為
的切線方程為![]() ,求實數
,求實數![]() 的值;
的值;
(2)若函數![]() 在區間
在區間![]() 上有兩個零點,求實數
上有兩個零點,求實數![]() 的取值范圍.
的取值范圍.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]()
【解析】
(1)根據解析式求得導函數,設切點坐標為![]() ,結合導數的幾何意義可得方程
,結合導數的幾何意義可得方程![]() ,構造函數
,構造函數![]() ,并求得
,并求得![]() ,由導函數求得
,由導函數求得![]() 有最小值
有最小值![]() ,進而可知由唯一零點
,進而可知由唯一零點![]() ,即可代入求得
,即可代入求得![]() 的值;
的值;
(2)將![]() 解析式代入
解析式代入![]() ,結合零點定義化簡并分離參數得
,結合零點定義化簡并分離參數得![]() ,構造函數
,構造函數![]() ,根據題意可知直線
,根據題意可知直線![]() 與曲線
與曲線![]() 有兩個交點;求得
有兩個交點;求得![]() 并令
并令![]() 求得極值點,列出表格判斷
求得極值點,列出表格判斷![]() 的單調性與極值,即可確定與
的單調性與極值,即可確定與![]() 有兩個交點時
有兩個交點時![]() 的取值范圍.
的取值范圍.
(1)依題意,![]() ,
,![]() ,
,
設切點為![]() ,
,![]() ,
,
故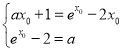 ,
,
故![]() ,則
,則![]() ;
;
令![]() ,
,![]() ,
,
故當![]() 時,
時,![]() ,
,
當![]() 時,
時,![]() ,
,
故當![]() 時,函數
時,函數![]() 有最小值,
有最小值,
由于![]() ,故
,故![]() 有唯一實數根0,
有唯一實數根0,
即![]() ,則
,則![]() ;
;
(2)由![]() ,得
,得![]() .
.
所以“![]() 在區間
在區間![]() 上有兩個零點”等價于“直線
上有兩個零點”等價于“直線![]() 與曲線
與曲線![]() 在
在![]() 有兩個交點”;
有兩個交點”;
由于![]() .
.
由![]() ,解得
,解得![]() ,
,![]() .
.
當![]() 變化時,
變化時,![]() 與
與![]() 的變化情況如下表所示:
的變化情況如下表所示:
|
|
|
| 3 |
|
|
| 0 | + | 0 |
|
|
| 極小值 |
| 極大值 |
|
所以![]() 在
在![]() ,
,![]() 上單調遞減,在
上單調遞減,在![]() 上單調遞增.
上單調遞增.
又因為![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
故當![]() 或
或![]() 時,直線
時,直線![]() 與曲線
與曲線![]() 在
在![]() 上有兩個交點,
上有兩個交點,
即當![]() 或
或![]() 時,函數
時,函數![]() 在區間
在區間![]() 上有兩個零點.
上有兩個零點.


科目:高中數學 來源: 題型:
【題目】某貧困地區幾個丘陵的外圍有兩條相互垂直的直線型公路![]() ,以及鐵路線上的一條應開鑿的直線穿山隧道
,以及鐵路線上的一條應開鑿的直線穿山隧道![]() ,為進一步改善山區的交通現狀,計劃修建一條連接兩條公路
,為進一步改善山區的交通現狀,計劃修建一條連接兩條公路![]() 和山區邊界的直線型公路
和山區邊界的直線型公路![]() , 以
, 以![]() 所在的直線分別為
所在的直線分別為![]() 軸,
軸,![]() 軸, 建立平面直角坐標系
軸, 建立平面直角坐標系![]() , 如圖所示, 山區邊界曲線為
, 如圖所示, 山區邊界曲線為![]() ,設公路
,設公路![]() 與曲線
與曲線![]() 相切于點
相切于點![]() ,
,![]() 的橫坐標為
的橫坐標為![]() .
.
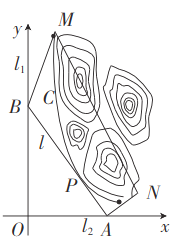
(1)當![]() 為何值時,公路
為何值時,公路![]() 的長度最短?求出最短長度;
的長度最短?求出最短長度;
(2)當公路![]() 的長度最短時,設公路
的長度最短時,設公路![]() 交
交![]() 軸,
軸,![]() 軸分別為
軸分別為![]() ,
,![]() 兩點,并測得四邊形
兩點,并測得四邊形![]() 中,
中,![]() ,
,![]() ,
,![]() 千米,
千米,![]() 千米,求應開鑿的隧道
千米,求應開鑿的隧道![]() 的長度.
的長度.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某企業對設備進行升級改造,現從設備改造前后生產的大量產品中各抽取了100件產品作為樣本,檢測一項質量指標值,該項質量指標值落在區間![]() 內的產品視為合格品,否則視為不合格品,如圖是設備改造前樣本的頻率分布直方圖,下表是設備改造后樣本的頻數分布表.
內的產品視為合格品,否則視為不合格品,如圖是設備改造前樣本的頻率分布直方圖,下表是設備改造后樣本的頻數分布表.
圖:設備改造前樣本的頻率分布直方圖
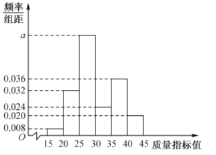
表:設備改造后樣本的頻率分布表
質量指標值 |
|
|
|
|
|
|
頻數 | 2 | 18 | 48 | 14 | 16 | 2 |
(1)求圖中實數![]() 的值;
的值;
(2)企業將不合格品全部銷毀后,對合格品進行等級細分,質量指標值落在區間![]() 內的定為一等品,每件售價240元;質量指標值落在區間
內的定為一等品,每件售價240元;質量指標值落在區間![]() 或
或![]() 內的定為二等品,每件售價180元;其他的合格品定為三等品,每件售價120元,根據表1的數據,用該組樣本中一等品、二等品、三等品各自在合格品中的頻率代替從所有產品中抽到一件相應等級產品的概率.若有一名顧客隨機購買兩件產品支付的費用為
內的定為二等品,每件售價180元;其他的合格品定為三等品,每件售價120元,根據表1的數據,用該組樣本中一等品、二等品、三等品各自在合格品中的頻率代替從所有產品中抽到一件相應等級產品的概率.若有一名顧客隨機購買兩件產品支付的費用為![]() (單位:元),求
(單位:元),求![]() 的分布列和數學期望.
的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】隨著智能手機的普及,手機計步軟件迅速流行開來,這類軟件能自動記載每日健步走的步數,從而為科學健身提供了一定幫助.某企業為了解員工每日健步走的情況,從該企業正常上班的員工中隨機抽取300名,統計他們的每日健步走的步數(均不低于4千步,不超過20千步).按步數分組,得到頻率分布直方圖如圖所示.
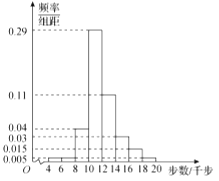
(1)求這300名員工日行步數![]() (單位:千步)的樣本平均數(每組數據以該組區間的中點值為代表,結果保留整數);
(單位:千步)的樣本平均數(每組數據以該組區間的中點值為代表,結果保留整數);
(2)由直方圖可以認為該企業員工的日行步數![]() (單位:千步)服從正態分布
(單位:千步)服從正態分布![]() ,其中
,其中![]() 為樣本平均數,標準差
為樣本平均數,標準差![]() 的近似值為2,求該企業被抽取的300名員工中日行步數
的近似值為2,求該企業被抽取的300名員工中日行步數![]() 的人數;
的人數;
(3)用樣本估計總體,將頻率視為概率.若工會從該企業員工中隨機抽取2人作為“日行萬步”活動的慰問獎勵對象,規定:日行步數不超過8千步者為“不健康生活方式者”,給予精神鼓勵,獎勵金額為每人0元;日行步數為8~14千步者為“一般生活方式者”,獎勵金額為每人100元;日行步數為14千步以上者為“超健康生活方式者”,獎勵金額為每人200元.求工會慰問獎勵金額![]() (單位:元)的分布列和數學期望.
(單位:元)的分布列和數學期望.
附:若隨機變量![]() 服從正態分布
服從正態分布![]() ,則
,則![]() ,
,![]()
![]() ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
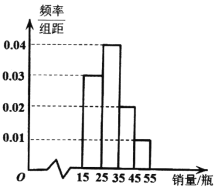
【題目】某早餐店對一款新口味的酸奶進行了一段時間試銷,定價為![]() 元/瓶.酸奶在試銷售期間足量供應,每天的銷售數據按照
元/瓶.酸奶在試銷售期間足量供應,每天的銷售數據按照![]() ,
,![]() ,
,![]() ,
,![]() 分組,得到如下頻率分布直方圖,以不同銷量的頻率估計概率.
分組,得到如下頻率分布直方圖,以不同銷量的頻率估計概率.
![]() 從試銷售期間任選三天,求其中至少有一天的酸奶銷量大于
從試銷售期間任選三天,求其中至少有一天的酸奶銷量大于![]() 瓶的概率;
瓶的概率;
![]() 試銷結束后,這款酸奶正式上市,廠家只提供整箱批發:大箱每箱
試銷結束后,這款酸奶正式上市,廠家只提供整箱批發:大箱每箱![]() 瓶,批發成本
瓶,批發成本![]() 元;小箱每箱
元;小箱每箱![]() 瓶,批發成本
瓶,批發成本![]() 元.由于酸奶保質期短,當天未賣出的只能作廢.該早餐店以試銷售期間的銷量作為參考,決定每天僅批發一箱(計算時每個分組取中間值作為代表,比如銷量為
元.由于酸奶保質期短,當天未賣出的只能作廢.該早餐店以試銷售期間的銷量作為參考,決定每天僅批發一箱(計算時每個分組取中間值作為代表,比如銷量為![]() 時看作銷量為
時看作銷量為![]() 瓶).
瓶).
①設早餐店批發一大箱時,當天這款酸奶的利潤為隨機變量![]() ,批發一小箱時,當天這款酸奶的利潤為隨機變量
,批發一小箱時,當天這款酸奶的利潤為隨機變量![]() ,求
,求![]() 和
和![]() 的分布列和數學期望;
的分布列和數學期望;
②以利潤作為決策依據,該早餐店應每天批發一大箱還是一小箱?
注:銷售額=銷量×定價;利潤=銷售額-批發成本.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】空氣質量指數AQI是反映空氣質量狀況的指數,AQI指數值越小,表明空氣質量越好,其對應關系如下表:
AQI指數值 | 0~50 | 51~100 | 101~150 | 151~200 | 201~300 | >300 |
空氣質量 | 優 | 良 | 輕度污染 | 中度污染 | 重度污染 | 嚴重污染 |
下圖是某市10月1日—20日AQI指數變化趨勢:

下列敘述錯誤的是
A. 這20天中AQI指數值的中位數略高于100
B. 這20天中的中度污染及以上的天數占![]()
C. 該市10月的前半個月的空氣質量越來越好
D. 總體來說,該市10月上旬的空氣質量比中旬的空氣質量好
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設橢圓![]() :
:![]() ,
,![]() 為左、右焦點,
為左、右焦點,![]() 為短軸端點,且
為短軸端點,且![]() ,離心率為
,離心率為![]() ,
,![]() 為坐標原點.
為坐標原點.
(1)求橢圓![]() 的方程,
的方程,
(2)是否存在圓心在原點的圓,使得該圓的任意一條切線與橢圓C恒有兩個交點![]() ,
,![]() ,且滿足
,且滿足![]() ?若存在,求出該圓的方程,若不存在,說明理由.
?若存在,求出該圓的方程,若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】十二生肖,又稱十二屬相,中國古人拿十二種動物來配十二地支,組成子鼠、丑牛、寅虎、卯兔、辰龍、已蛇、午馬、未羊、申猴、西雞、戌狗、亥豬十二屬相現有十二生肖吉祥物各一件,甲、乙、丙三位同學依次隨機抽取一件作為禮物,甲同學喜歡馬、牛,乙同學喜歡馬、龍、狗,丙同學除了鼠不喜歡外其他的都喜歡,則這三位同學抽取的禮物都喜歡的概率是_____.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的長軸長為4,直線
的長軸長為4,直線![]() 被橢圓
被橢圓![]() 截得的線段長為
截得的線段長為![]() .
.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)過橢圓![]() 的右頂點作互相垂直的兩條直線
的右頂點作互相垂直的兩條直線![]() 分別交橢圓
分別交橢圓![]() 于
于![]() 兩點(點
兩點(點![]() 不同于橢圓
不同于橢圓![]() 的右頂點),證明:直線
的右頂點),證明:直線![]() 過定點
過定點![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com