
【題目】在銳角△ABC中,a=2![]() ,_______,求△ABC的周長l的范圍.
,_______,求△ABC的周長l的范圍.
在①![]() (﹣cos
(﹣cos![]() ,sin
,sin![]() ),
),![]() (cos
(cos![]() ,sin
,sin![]() ),且
),且![]()
![]() ,②cosA(2b﹣c)=acosC,③f(x)=cosxcos(x
,②cosA(2b﹣c)=acosC,③f(x)=cosxcos(x![]() )
)![]() ,f(A)
,f(A)![]()
注:這三個條件中任選一個,補充在上面問題中并對其進行求解.
【答案】l△ABC∈(6+2![]() ,6
,6![]() ].
].
【解析】
選①時,由平面向量的數量積與三角恒等變換求出A的值,再利用正弦定理和三角恒等變換求出△ABC周長的取值范圍;
選②時,由正弦定理和三角恒等變換求出A的值,再利用正弦定理和三角恒等變換求出△ABC周長的取值范圍;
選③時,由三角恒等變換求得A的值,再利用正弦定理和三角恒等變換求出△ABC周長的取值范圍.
解:若選①,則由![]() (﹣cos
(﹣cos![]() ,sin
,sin![]() ),
),![]() (cos
(cos![]() ,sin
,sin![]() ),且
),且![]()
![]() ,
,
得![]() ,∴cosA
,∴cosA![]() ,
,
又A∈(0,![]() ),
),
所以A![]() ;
;
又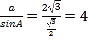 ,所以
,所以![]() ,
,![]() ,
,
△ABC的周長為![]()
![]()
![]() ,
,
即![]() ;
;
因為銳角△ABC中,A![]() ,所以
,所以![]() ,
,![]() ,
,
所以B∈(![]() ,
,![]() ),
),
所以B![]() ∈(
∈(![]() ,
,![]() ),
),
所以△ABC的周長為l△ABC∈(6+2![]() ,6
,6![]() ].
].
若選②,由cos A(2b﹣c)=acos C,
所以2bcosA=acosC+ccosA,
所以2sinBcosA=sinAcosC+cosAsinC=sin(A+C)=sinB;
又B∈(0,π),所以sinB≠0,所以cosA![]() ;
;
又A∈(0,![]() ),所以A
),所以A![]() ;
;
又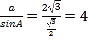 ,所以
,所以![]() ,
,![]() ,
,
△ABC的周長為![]()
![]()
![]() ,
,
即![]() ;
;
因為銳角△ABC中,A![]() ,所以
,所以![]() ,
,![]() ,
,
所以B∈(![]() ,
,![]() ),
),
所以B![]() ∈(
∈(![]() ,
,![]() ),
),
所以△ABC的周長為l△ABC∈(6+2![]() ,6
,6![]() ].
].
若選③,則f(x)=cos xcos(x![]() )
)![]()
![]()
![]()
![]() cos xsin x
cos xsin x![]()
![]()
![]() (
(![]() cos2x
cos2x![]() sin2x)
sin2x)
![]() sin(2x
sin(2x![]() ),
),
又f(A)![]() ,所以sin(2A
,所以sin(2A![]() )
)![]() ,
,
又A∈(0,![]() ),所以A
),所以A![]() ;
;
又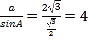 ,所以
,所以![]() ,
,![]() ,
,
△ABC的周長為![]()
![]()
![]() ,
,
即![]() ;
;
因為銳角△ABC中,A![]() ,所以
,所以![]() ,
,![]() ,
,
所以B∈(![]() ,
,![]() ),
),
所以B![]() ∈(
∈(![]() ,
,![]() ),
),
所以△ABC的周長為l△ABC∈(6+2![]() ,6
,6![]() ].
].


 千里馬走向假期期末仿真試卷寒假系列答案
千里馬走向假期期末仿真試卷寒假系列答案科目:高中數學 來源: 題型:
【題目】如圖,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,D為線段BC(端點除外)上一動點.現將
,D為線段BC(端點除外)上一動點.現將![]() 沿線段AD折起至
沿線段AD折起至![]() ,使二面角
,使二面角![]() 的大小為120°,則在點D的移動過程中,下列說法錯誤的是( )
的大小為120°,則在點D的移動過程中,下列說法錯誤的是( )

A.不存在點![]() ,使得
,使得![]()
B.點![]() 在平面
在平面![]() 上的投影軌跡是一段圓弧
上的投影軌跡是一段圓弧
C.![]() 與平面
與平面![]() 所成角的余弦值的取值范圍是
所成角的余弦值的取值范圍是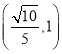
D.線段![]() 的最小值是
的最小值是![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列![]() ,其中
,其中![]() .
.
(1)若![]() 滿足
滿足![]() .
.
①當![]() ,且
,且![]() 時,求
時,求![]() 的值;
的值;
②若存在互不相等的正整數![]() ,滿足
,滿足![]() ,且
,且![]() 成等差數列,求
成等差數列,求![]() 的值.
的值.
(2)設數列![]() 的前
的前![]() 項和為
項和為![]() ,數列
,數列![]() 的前n項和為
的前n項和為![]() ,
,![]() ,
,![]() ,若
,若![]() ,
,![]() ,且
,且![]() 恒成立,求
恒成立,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知如圖所示的三棱錐D﹣ABC的四個頂點均在球O的球面上,△ABC和△DBC所在平面相互垂直,AB=3,AC=![]() ,BC=CD=BD=2
,BC=CD=BD=2![]() ,則球O的表面積為( )
,則球O的表面積為( )
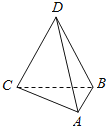
A.4π B.12π C.16π D.36π
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】新冠病毒是一種通過飛沫和接觸傳播的變異病毒,為篩查該病毒,有一種檢驗方式是檢驗血液樣本相關指標是否為陽性,對于![]() 份血液樣本,有以下兩種檢驗方式:一是逐份檢驗,則需檢驗
份血液樣本,有以下兩種檢驗方式:一是逐份檢驗,則需檢驗![]() 次.二是混合檢驗,將其中
次.二是混合檢驗,將其中![]() 份血液樣本分別取樣混合在一起,若檢驗結果為陰性,那么這
份血液樣本分別取樣混合在一起,若檢驗結果為陰性,那么這![]() 份血液全為陰性,因而檢驗一次就夠了;如果檢驗結果為陽性,為了明確這
份血液全為陰性,因而檢驗一次就夠了;如果檢驗結果為陽性,為了明確這![]() 份血液究竟哪些為陽性,就需要對它們再逐份檢驗,此時
份血液究竟哪些為陽性,就需要對它們再逐份檢驗,此時![]() 份血液檢驗的次數總共為
份血液檢驗的次數總共為![]() 次.某定點醫院現取得4份血液樣本,考慮以下三種檢驗方案:方案一,逐個檢驗;方案二,平均分成兩組檢驗;方案三,四個樣本混在一起檢驗.假設在接受檢驗的血液樣本中,每份樣本檢驗結果是陽性還是陰性都是相互獨立的,且每份樣本是陰性的概率為
次.某定點醫院現取得4份血液樣本,考慮以下三種檢驗方案:方案一,逐個檢驗;方案二,平均分成兩組檢驗;方案三,四個樣本混在一起檢驗.假設在接受檢驗的血液樣本中,每份樣本檢驗結果是陽性還是陰性都是相互獨立的,且每份樣本是陰性的概率為![]() .
.
(Ⅰ)求把2份血液樣本混合檢驗結果為陽性的概率;
(Ⅱ)若檢驗次數的期望值越小,則方案越“優”.方案一、二、三中哪個最“優”?請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某學生為了測試煤氣灶燒水如何節省煤氣的問題設計了一個實驗,并獲得了煤氣開關旋鈕旋轉的弧度數![]() 與燒開一壺水所用時間
與燒開一壺水所用時間![]() 的一組數據,且作了一定的數據處理(如表),得到了散點圖(如圖).
的一組數據,且作了一定的數據處理(如表),得到了散點圖(如圖).

|
|
|
|
|
|
|
1.47 | 20.6 | 0.78 | 2.35 | 0.81 | -19.3 | 16.2 |
表中![]() ,
,![]() .
.
(1)根據散點圖判斷,![]() 與
與![]() 哪一個更適宜作燒開一壺水時間
哪一個更適宜作燒開一壺水時間![]() 關于開關旋鈕旋轉的弧度數
關于開關旋鈕旋轉的弧度數![]() 的回歸方程類型?(不必說明理由)
的回歸方程類型?(不必說明理由)
(2)根據判斷結果和表中數據,建立關于
![]() 的回歸方程;
的回歸方程;
(3)若旋轉的弧度數![]() 與單位時間內煤氣輸出量
與單位時間內煤氣輸出量![]() 成正比,那么
成正比,那么![]() 為多少時燒開一壺水最省煤氣?
為多少時燒開一壺水最省煤氣?
附:對于一組數據![]()
![]()
![]() ,…,
,…,![]() ,其回歸直線
,其回歸直線![]() 的斜率和截距的最小二乘估計分別為
的斜率和截距的最小二乘估計分別為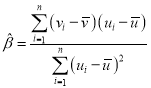 ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() .
.
(1)求函數![]() 的圖象在
的圖象在![]() (
(![]() 為自然對數的底數)處的切線方程;
為自然對數的底數)處的切線方程;
(2)若對任意的![]() ,均有
,均有![]() ,則稱
,則稱![]() 為
為![]() 在區間
在區間![]() 上的下界函數,
上的下界函數,![]() 為
為![]() 在區間
在區間![]() 上的上界函數.
上的上界函數.
①若![]() ,求證:
,求證:![]() 為
為![]() 在
在![]() 上的上界函數;
上的上界函數;
②若![]() ,
,![]() 為
為![]() 在
在![]() 上的下界函數,求實數
上的下界函數,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com