
(本小題共14分)如圖,四棱錐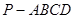 中,底面
中,底面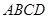 為平行四邊形,
為平行四邊形,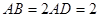 ,
,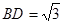 ,
, ⊥底面
⊥底面 .
.

(1)證明:平面 平面
平面 ;
;
(2)若二面角 為
為 ,求
,求 與平面
與平面 所成角的正弦值。
所成角的正弦值。
(1)見解析;(2)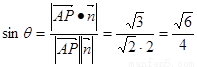
【解析】本試題主要是考查了面面垂直的證明,以及二面角的求解的綜合運用。
(1)利用線面垂直的的判定定理和面面垂直的判定定理得到鄭敏。
(2)合理的建立空間直角坐標系,可以表示出平面的法向量和法向量的夾角,然后借助于向量的數量積公式的得到二面角的平面角的求解。
解:(1)∵ ∴
∴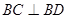
又∵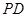 ⊥底面
⊥底面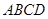 ∴
∴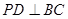
又∵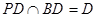 ∴
∴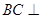 平面
平面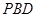 而
而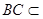 平面
平面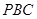
∴平面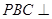 平面
平面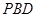 …………6分
…………6分
(2)由(1)所證,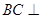 平面
平面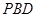
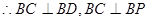
所以∠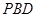 即為二面角P-BC-D的平面角,即∠
即為二面角P-BC-D的平面角,即∠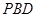
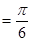 ………………7分
………………7分
而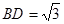 ,所以
,所以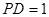
分別以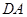 、
、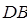 、
、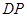 為
為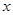 軸、
軸、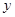 軸、
軸、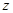 軸建立空間直角坐標系。……………8分
軸建立空間直角坐標系。……………8分
則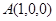 ,
,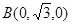 ,
,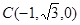 ,
, 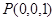
所以, ,
,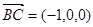 ,
,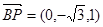 ……………10分
……………10分
設平面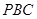 的法向量為
的法向量為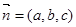 ,則
,則
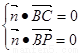
即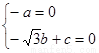 可解得
可解得 ……………12分
……………12分
∴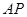 與平面
與平面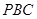 所成角的正弦值為
所成角的正弦值為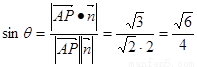 ………14分
………14分
(另外做出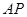 與平面
與平面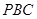 所成角或利用等體積求出也可)
所成角或利用等體積求出也可)


科目:高中數學 來源: 題型:
(07年北京卷理)(本小題共14分)
如圖,在![]() 中,
中,![]() ,斜邊
,斜邊![]() .
.![]() 可以通過
可以通過![]() 以直線
以直線![]() 為軸旋轉得到,且二面角
為軸旋轉得到,且二面角![]() 是直二面角.動點
是直二面角.動點![]() 的斜邊
的斜邊![]() 上.
上.

(I)求證:平面![]() 平面
平面![]() ;
;
(II)當![]() 為
為![]() 的中點時,求異面直線
的中點時,求異面直線![]() 與
與![]() 所成角的大小;
所成角的大小;
(III)求![]() 與平面
與平面![]() 所成角的最大值.
所成角的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
(07年北京卷文)(本小題共14分)
如圖,在![]() 中,
中,![]() ,斜邊
,斜邊![]() .
.![]() 可以通過
可以通過![]() 以直線
以直線![]() 為軸旋轉得到,且二面角
為軸旋轉得到,且二面角![]() 的直二面角.
的直二面角.![]() 是
是![]() 的中點.
的中點.

(I)求證:平面![]() 平面
平面![]() ;
;
(II)求異面直線![]() 與
與![]() 所成角的大小.
所成角的大小.
查看答案和解析>>
科目:高中數學 來源:2011-2012學年北京市豐臺區高三上學期期末考試理科數學 題型:解答題
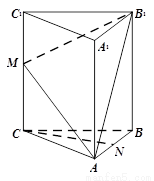
(本小題共14分)如圖,在三棱柱ABC-A1B1C1中,CC1⊥底面ABC,AC=BC=2,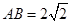 ,CC1=4,M是棱CC1上一點.
,CC1=4,M是棱CC1上一點.
(Ⅰ)求證:BC⊥AM;
(Ⅱ)若M,N分別是CC1,AB的中點,求證:CN //平面AB1M;
(Ⅲ)若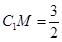 ,求二面角A-MB1-C的大小.
,求二面角A-MB1-C的大小.
查看答案和解析>>
科目:高中數學 來源:2011-2012學年北京市豐臺區高三上學期期末考試文科數學 題型:解答題
(本小題共14分)如圖,在三棱柱ABC-A1B1C1中,CC1⊥底面ABC,AC=BC,M,N分別是CC1,AB的中點.
(Ⅰ)求證:CN⊥AB1;
(Ⅱ)求證:CN //平面AB1M.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com