
【題目】已知點![]() 是拋物線
是拋物線![]() 的焦點,若點
的焦點,若點![]() 在拋物線
在拋物線![]() 上,且
上,且![]()
![]() 求拋物線
求拋物線![]() 的方程;
的方程;
![]() 動直線
動直線![]() 與拋物線
與拋物線![]() 相交于
相交于![]() 兩點,問:在
兩點,問:在![]() 軸上是否存在定點
軸上是否存在定點![]() 其中
其中![]() ,使得向量
,使得向量![]() 與向量
與向量![]() 共線
共線![]() 其中
其中![]() 為坐標原點
為坐標原點![]() ?若存在,求出點
?若存在,求出點![]() 的坐標;若不存在,請說明理由.
的坐標;若不存在,請說明理由.
【答案】(1)![]() ;(2)存在,
;(2)存在,![]() .
.
【解析】
![]() 求得拋物線的焦點和準線方程,運用拋物線的定義可得
求得拋物線的焦點和準線方程,運用拋物線的定義可得![]() 的坐標,代入拋物線方程,解得
的坐標,代入拋物線方程,解得![]() ,進而得到拋物線的方程;
,進而得到拋物線的方程;![]() 在
在![]() 軸上假設存在定點
軸上假設存在定點![]() 其中
其中![]() ,使得
,使得![]() 與向量
與向量![]() 共線,可得
共線,可得![]() 軸平分
軸平分![]() ,設
,設![]() ,
,![]() ,聯立
,聯立![]() 和
和![]() ,根據
,根據![]() 恒成立,運用韋達定理和直線的斜率公式,化簡整理可得
恒成立,運用韋達定理和直線的斜率公式,化簡整理可得![]() 的方程,求得
的方程,求得![]() ,可得結論.
,可得結論.
![]() 拋物線C:
拋物線C:![]() 的焦點為
的焦點為![]() ,
,
準線方程為![]() ,
,
即有![]() ,即
,即![]() ,
,
則![]() ,解得
,解得![]() ,
,
則拋物線的方程為![]() ;
;
![]() 在x軸上假設存在定點
在x軸上假設存在定點![]() 其中
其中![]() ,
,
使得![]() 與向量
與向量![]() 共線,
共線,
由![]() ,
,![]() 均為單位向量,且它們的和向量與
均為單位向量,且它們的和向量與![]() 共線,
共線,
可得x軸平分![]() ,
,
設![]() ,
,![]() ,
,
聯立![]() 和
和![]() ,
,
得![]() ,
,
![]() 恒成立.
恒成立.
![]() ,
,![]()
設直線DA、DB的斜率分別為![]() ,
,![]() ,
,
則由![]() 得,
得,
![]()
![]() ,
,
![]() ,
,![]()
聯立![]() ,得
,得![]() ,
,
故存在![]() 滿足題意,
滿足題意,
綜上,在x軸上存在一點![]() ,使得x軸平分
,使得x軸平分![]() ,
,
即![]() 與向量
與向量![]() 共線.
共線.


 同步練習強化拓展系列答案
同步練習強化拓展系列答案科目:高中數學 來源: 題型:
【題目】過拋物線![]() 的焦點
的焦點![]() 的直線交拋物線
的直線交拋物線![]() 于兩點
于兩點![]() ,線段
,線段![]() 的中點為
的中點為![]() .
.
(1)求動點![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(2)經過坐標原點![]() 的直線
的直線![]() 與軌跡
與軌跡![]() 交于
交于![]() 兩點,與拋物線
兩點,與拋物線![]() 交于
交于![]() 點(
點(![]() ),若
),若![]() ,求直線
,求直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
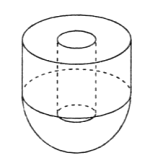
【題目】如圖所示,某幾何體由底面半徑和高均為5的圓柱與半徑為5的半球面對接而成,該封閉幾何體內部放入一個小圓柱體,且圓柱體的上下底面均與外層圓柱的底面平行,則小圓柱體積的最大值為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某公司租地建倉庫,每月土地占用費y1與倉庫到車站的距離成反比,而每月庫存貨物的運費y2與到車站的距離成正比,如果在距離車站10km處建倉庫,這兩項費用y1和y2分別為2萬元和8萬元,那么要使這兩項費用之和最小,倉庫應建在距離車站( )
A.4kmB.5kmC.6kmD.7km
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】對稱軸為坐標軸的橢圓![]() 的焦點為
的焦點為![]() ,
,![]() ,
,![]() 在
在![]() 上.
上.
(1)求橢圓![]() 的方程;
的方程;
(2)設不過原點![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 交于
交于![]() ,
,![]() 兩點,且直線
兩點,且直線![]() ,
,![]() ,
,![]() 的斜率依次成等比數列,則當
的斜率依次成等比數列,則當![]() 的面積為
的面積為![]() 時,求直線
時,求直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校高一舉行了一次數學競賽,為了了解本次競賽學生的成績情況,從中抽取了部分學生的分數(得分取正整數,滿分為![]() )作為樣本(樣本容量為
)作為樣本(樣本容量為![]() )進行統計,按照[50,60),[60,70),[70,80),[80,90),[90,100]的分組作出頻率分布直方圖,已知得分在[50,60),[90,100]的頻數分別為8,2.
)進行統計,按照[50,60),[60,70),[70,80),[80,90),[90,100]的分組作出頻率分布直方圖,已知得分在[50,60),[90,100]的頻數分別為8,2.

(1)求樣本容量![]() 和頻率分布直方圖中的
和頻率分布直方圖中的![]() 的值;
的值;
(2)估計本次競賽學生成績的中位數;
(3)在選取的樣本中,從競賽成績在![]() 分以上(含
分以上(含![]() 分)的學生中隨機抽取
分)的學生中隨機抽取![]() 名學生,求所抽取的
名學生,求所抽取的![]() 名學生中至少有一人得分在
名學生中至少有一人得分在![]() 內的概率.
內的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,
,
(1)若對任意![]() ,
,![]() 且
且![]() ,都有
,都有![]() ,求實數
,求實數![]() 的取值范圍;
的取值范圍;
(2)在第(1)問求出的實數![]() 的范圍內,若存在一個與
的范圍內,若存在一個與![]() 有關的負數
有關的負數![]() ,使得對任意
,使得對任意![]() 時
時![]() 恒成立,求
恒成立,求![]() 的最小值及相應的
的最小值及相應的![]() 值.
值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com