【題目】某商場舉行促銷活動，有兩個摸獎箱，
箱內有一個“
”號球，兩個“
”號球，三個“
”號球、四個無號球，
箱內有五個“”號球，五個“”號球，每次摸獎后放回，每位顧客消費額滿
元有一次箱內摸獎機會，消費額滿
元有一次箱內摸獎機會，摸得有數字的球則中獎，“”號球獎
元，“”號球獎
元，“”號球獎
元，摸得無號球則沒有獎金。
（1）經統計，顧客消費額
服從正態分布
，某天有
位顧客，請估計消費額（單位：元）在區間
內并中獎的人數.（結果四舍五入取整數）
附：若
，則
，
.
（2）某三位顧客各有一次箱內摸獎機會，求其中中獎人數
的分布列.
（3）某顧客消費額為
元，有兩種摸獎方法，
方法一：三次箱內摸獎機會；
方法二：一次箱內摸獎機會.
請問：這位顧客選哪一種方法所得獎金的期望值較大.
【答案】(1) 中獎的人數約為
人.
(2)分布列見解析.
(3) 這位顧客選方法二所得獎金的期望值較大.
【解析】分析：（1）依題意得
，
，得
，消費額
在區間
內的顧客有一次
箱內摸獎機會，中獎率為
，人數約
，可得其中中獎的人數；（2）三位顧客每人一次箱內摸獎中獎率都為，三人中中獎人數服
從二項分布
，
，
，從而可得分布列；（3）利用數學期望的計算公式算出兩種方法所得獎金的期望值即可得出結論.
詳解：（1）依題意得，，
得，消費額在區間內的顧客有一次箱內摸獎機會，中獎率為
人數約
人
其中中獎的人數約為
人
（2）三位顧客每人一次箱內摸獎中獎率都為，
三人中中獎人數服從二項分布，，
故的分布列為
|
|
|
|
|
|
|
|
|
|
（3）箱摸一次所得獎金的期望為
箱摸一次所得獎金的期望為
方法一所得獎金的期望值為
，
方法二所得獎金的期望值為
，
所以這位顧客選方法二所得獎金的期望值較大
科目：高中數學 來源： 題型：
【題目】如圖，四棱錐P一ABCD中，AB=AD=2BC=2，BC∥AD，AB⊥AD，△PBD為正三角形．且PA=2
．
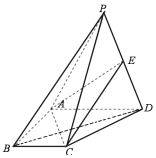
（1）證明：平面PAB⊥平面PBC；
（2）若點P到底面ABCD的距離為2，E是線段PD上一點，且PB∥平面ACE，求四面體A-CDE的體積．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在平面直角坐標系
中，曲線
的參數方程為
（
為參數），以坐標原點
為極點，
軸的非負半軸為極軸且取相同的單位長度建立極坐標系，直線
的極坐標方程為
.
（1）寫出曲線的普通方程和直線的直角坐標方程；
（2）若直線與曲線相交于
、
兩點，求
的面積.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在四棱錐
中，底面
為矩形，側面
底面，
為棱
的中點，
為棱
上任意一點，且不與
點、
點重合．
．
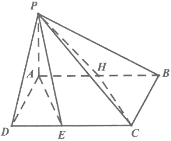
（1）求證：平面
平面；
（2）是否存在點使得平面
與平面
所成的角的余弦值為
？若存在，求出點的位置；若不存在，請說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知數列{an}的首項
， 
， 
．
(1)求證：數列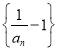
為等比數列；
(2)記
，若Sn<100，求最大正整數n；
(3)是否存在互不相等的正整數m，s，n，使m，s，n成等差數列，且am－1，as－1，an－1成等比數列？如果存在，請給以證明；如果不存在，請說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數
，
．
（1）若
在點
處的切線與直線
垂直，求函數在
點處的切線方程；
（2）若對于
，
恒成立，求正實數
的取值范圍；
（3）設函數
，且函數
有極大值點
，求證：
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
