
(08年湖北卷理)(本小題滿分14分)
已知數列{an}和{bn}滿足:a1=λ,an+1=![]() 其中λ為實數,n為正整數.
其中λ為實數,n為正整數.
(Ⅰ)對任意實數λ,證明數列{an}不是等比數列;
(Ⅱ)試判斷數列{bn}是否為等比數列,并證明你的結論;
(Ⅲ)設0<a<b,Sn為數列{bn}的前n項和.是否存在實數λ,使得對任意正整數n,都有
a<Sn<b?若存在,求λ的取值范圍;若不存在,說明理由.
(1)證明;假設存在一個實數![]() ,使
,使![]() 是等比數列,則有
是等比數列,則有![]() ,
,
即![]() 矛盾。
矛盾。
所以![]() 不是等比數列。
不是等比數列。
(2)解:因為
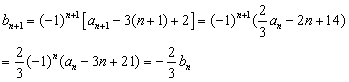
又![]() ,所以
,所以
當![]() 時,
時,![]() 些時
些時![]() 不是等比數列;
不是等比數列;
當![]() 時,
時,![]() 由上可知
由上可知![]() 。
。
故當![]() 時,數列
時,數列![]() 是以
是以![]() 為首項,
為首項,![]() 為公比的等比數列。
為公比的等比數列。
(3)由(2)知,當![]() 時,
時,![]() 不滿足題目要求。
不滿足題目要求。
![]() ,故得
,故得![]() 可得
可得
![]() 。
。
要使![]() 對任意正整數
對任意正整數![]() 成立
成立
即![]()
得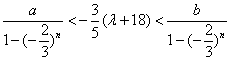 ......①
......①
令![]() ,則
,則
當![]() 為正奇數時,
為正奇數時,![]() ;當
;當![]() 為正偶數時,
為正偶數時,![]() .
.
所以![]() 的最大值為
的最大值為![]() ,
,![]() 的最小值為
的最小值為![]() ,
,
于是,由式①得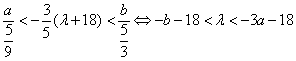 .
.
當![]() 時,由
時,由![]() 知,不存在實數
知,不存在實數![]() 滿足題目要求;
滿足題目要求;
當時![]() ,存在實數
,存在實數![]() ,使得對任意正整數
,使得對任意正整數![]() ,都有
,都有![]() ,且
,且![]() 的取值范圍是
的取值范圍是![]() 。
。
【試題解析】第(1)問問的是證明![]() “不是等比數列”,這樣的問題顯然用“反證法”;第(2)正著問,那就順著推;第(3)問要先求和再解建立不等式。
“不是等比數列”,這樣的問題顯然用“反證法”;第(2)正著問,那就順著推;第(3)問要先求和再解建立不等式。
【高考考點】本題主要考查等比數列的定義、數列求和、不等式基礎知識和分類討論的思想,考查綜合分析問題的能力和推理能力。
【易錯提醒】本題主要是,沒有掌握解題的基本方法,再就是沒有分類討論。
【備考提示】對等比數列、等差數列、數求和的知識要熟練掌握,數列中要特別注意遞推關系式的結構。


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
(08年湖北卷理)(本小題滿分12分)
水庫的蓄水量隨時間而變化,現(xiàn)用t表示時間,以月為單位,年初為起點,根據歷年數據,某水庫的蓄水量(單位:億立方米)關于t的近似函數關系式為
V(t)=
(Ⅰ)該水庫的蓄求量小于50的時期稱為枯水期.以i-1<t<t表示第1月份(i=1,2,…,12),同一年內哪幾個月份是枯水期?
(Ⅱ)求一年內該水庫的最大蓄水量(取e=2.7計算)
查看答案和解析>>
科目:高中數學 來源: 題型:
(08年湖北卷理)(本小題滿分13分)
如圖,在以點O為圓心,|AB|=4為直徑的半圓ADB中,OD⊥AB,P是半圓弧上一點,
∠POB=30°,曲線C是滿足||MA|-|MB||為定值的動點M的軌跡,且曲線C過點P.
(Ⅰ)建立適當的平面直角坐標系,求曲線C的方程;
(Ⅱ)設過點D的直線l與曲線C相交于不同的兩點E、F.
若△OEF的面積不小于2![]() ,求直線l斜率的取值范圍.
,求直線l斜率的取值范圍.

查看答案和解析>>
科目:高中數學 來源: 題型:
(08年湖北卷理)(本小題滿分12分)
如圖,在直三棱柱![]() 中,平面
中,平面![]() 側面
側面![]()
(Ⅰ)求證: ![]()
(Ⅱ)若直線AC與平面A1BC所成的角為θ,二面角A1-BC-A的大小為φ的大小關系,并予以證明.

查看答案和解析>>
科目:高中數學 來源: 題型:
(08年湖北卷理)(本小題滿分12分)
如圖,在直三棱柱![]() 中,平面
中,平面![]() 側面
側面![]()
(Ⅰ)求證: ![]()
(Ⅱ)若直線AC與平面A1BC所成的角為θ,二面角A1-BC-A的大小為φ的大小關系,并予以證明.

查看答案和解析>>
科目:高中數學 來源: 題型:
(08年湖北卷理)(本小題滿分12分)
袋中有20個大小相同的球,其中記上0號的有10個,記上n號的有n個(n=1,2,3,4).現(xiàn)從袋中任取一球.ξ表示所取球的標號.
(Ⅰ)求ξ的分布列,期望和方差;
(Ⅱ)若η=aξ-b,Eη=1,Dη=11,試求a,b的值.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com