
【題目】已知數(shù)列{an}的前n項(xiàng)和是Sn,且Sn![]() =1(n∈N),數(shù)列{bn}是公差d不等于0的等差數(shù)列,且滿(mǎn)足:b1=
=1(n∈N),數(shù)列{bn}是公差d不等于0的等差數(shù)列,且滿(mǎn)足:b1=![]() ,而b2,b5,ba14成等比數(shù)列.
,而b2,b5,ba14成等比數(shù)列.
(1)求數(shù)列{an}、{bn}的通項(xiàng)公式;
(2)設(shè)cn=anbn,求數(shù)列{cn}的前n項(xiàng)和Tn.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]()
【解析】分析:(I)Sn![]() =1(n∈N),n≥2時(shí),Sn﹣1+
=1(n∈N),n≥2時(shí),Sn﹣1+![]() an﹣1=1,相減可得:an
an﹣1=1,相減可得:an![]() ﹣
﹣![]() an﹣1=0,化為:an=
an﹣1=0,化為:an=![]() an﹣1.利用等比數(shù)列的通項(xiàng)公式可得an.?dāng)?shù)列{bn}是公差d不等于0的等差數(shù)列,且滿(mǎn)足:b1=
an﹣1.利用等比數(shù)列的通項(xiàng)公式可得an.?dāng)?shù)列{bn}是公差d不等于0的等差數(shù)列,且滿(mǎn)足:b1=![]() =1.由b2,b5,b14成等比數(shù)列.可得
=1.由b2,b5,b14成等比數(shù)列.可得![]() =b2b14,(1+4d)2=(1+d)(1+13d),d≠0.解得d.即可得出;(Ⅱ)設(shè)cn=anbn=
=b2b14,(1+4d)2=(1+d)(1+13d),d≠0.解得d.即可得出;(Ⅱ)設(shè)cn=anbn=![]() ,利用錯(cuò)位相減法即可得出.
,利用錯(cuò)位相減法即可得出.
詳解:
(1)Sn![]() =1(n∈N),n≥2時(shí),Sn﹣1+
=1(n∈N),n≥2時(shí),Sn﹣1+![]() an﹣1=1,相減可得:an
an﹣1=1,相減可得:an![]() ﹣
﹣![]() an﹣1=0,化為:an=
an﹣1=0,化為:an=![]() an﹣1.
an﹣1.
n=1時(shí),a1+![]() =1,解得a1=
=1,解得a1=![]() .
.
∴數(shù)列{an}是等比數(shù)列,首項(xiàng)為![]() ,公比為
,公比為![]() .∴an=
.∴an=![]() =2×
=2×![]() .
.
數(shù)列{bn}是公差d不等于0的等差數(shù)列,且滿(mǎn)足:b1=![]() =1.
=1.
∵b2,b5,b14成等比數(shù)列.∴![]() =b2b14,
=b2b14,
∴(1+4d)2=(1+d)(1+13d),d≠0.解得d=2.∴bn=1+2(n﹣1)=2n﹣1.
(2)設(shè)cn=anbn=![]() .
.
求數(shù)列{cn}的前n項(xiàng)和Tn=![]() +……+
+……+![]() .
.
![]() =
=![]() +……+
+……+![]() +
+![]() ,
,
相減可得:![]() Tn=
Tn=![]() +4
+4![]() ﹣
﹣![]() =
=![]() +4×
+4×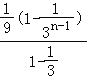 ﹣
﹣![]() ,
,
化為:Tn=2﹣![]() .
.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖是函數(shù)y=f(x)的導(dǎo)函數(shù)y=f′(x)的圖象,則下面判斷正確的是( )
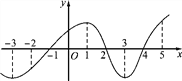
A. 在(-2,1)上f(x)是增函數(shù) B. 在(1,3)上f(x)是減函數(shù)
C. 當(dāng)x=2時(shí),f(x)取極大值 D. 當(dāng)x=4時(shí),f(x)取極大值
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)![]() .
.
(1)求函數(shù)![]() 的最小正周期與單調(diào)遞減區(qū)間;
的最小正周期與單調(diào)遞減區(qū)間;
(2)若函數(shù)![]() 的圖象上的所有點(diǎn)的橫坐標(biāo)伸長(zhǎng)到原來(lái)的
的圖象上的所有點(diǎn)的橫坐標(biāo)伸長(zhǎng)到原來(lái)的![]() 倍,所得的圖象與直線(xiàn)
倍,所得的圖象與直線(xiàn)![]() 交點(diǎn)的橫坐標(biāo)由小到大依次是
交點(diǎn)的橫坐標(biāo)由小到大依次是![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知圓![]() ,圓
,圓![]() ,經(jīng)過(guò)原點(diǎn)的兩直線(xiàn)
,經(jīng)過(guò)原點(diǎn)的兩直線(xiàn)![]() 滿(mǎn)足
滿(mǎn)足![]() ,且
,且![]() 交圓
交圓![]() 于不同兩點(diǎn)交
于不同兩點(diǎn)交![]() ,
, ![]() 圓
圓![]() 于不同兩點(diǎn)
于不同兩點(diǎn)![]() ,記
,記![]() 的斜率為
的斜率為![]()
(1)求![]() 的取值范圍;
的取值范圍;
(2)若四邊形![]() 為梯形,求
為梯形,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知三棱錐S﹣ABC的各頂點(diǎn)都在一個(gè)半徑為r的球面上,且SA=SB=SC=1,AB=BC=AC=![]() ,則球的表面積為( )
,則球的表面積為( )
A. 12π B. 8π C. 4π D. 3π
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)![]() ,(
,(![]() ).
).
(1)當(dāng)![]() ,且
,且![]() 時(shí),求
時(shí),求![]() 的值域;
的值域;
(2)若存在實(shí)數(shù)![]() 使得
使得![]() 成立,求實(shí)數(shù)
成立,求實(shí)數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】設(shè)![]() ,函數(shù)
,函數(shù)![]() .
.
(1)求![]() 的單調(diào)遞增區(qū)間;
的單調(diào)遞增區(qū)間;
(2)設(shè)![]() ,問(wèn)
,問(wèn)![]() 是否存在極值,若存在,請(qǐng)求出極值,若不存在,請(qǐng)說(shuō)明理由;
是否存在極值,若存在,請(qǐng)求出極值,若不存在,請(qǐng)說(shuō)明理由;
(3)設(shè)![]() 是函數(shù)
是函數(shù)![]() 圖象上任意不同的兩點(diǎn),線(xiàn)段
圖象上任意不同的兩點(diǎn),線(xiàn)段![]() 的中點(diǎn)為
的中點(diǎn)為![]() ,直線(xiàn)
,直線(xiàn)![]() 的斜率為
的斜率為![]() ,證明:
,證明:![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】某水產(chǎn)養(yǎng)殖基地要將一批海鮮用汽車(chē)從所在城市甲運(yùn)至銷(xiāo)售商所在城市乙,已知從城市甲到城市乙只有兩條公路,且運(yùn)費(fèi)由水產(chǎn)養(yǎng)殖基地承擔(dān).若水產(chǎn)養(yǎng)殖基地恰能在約定日期(×月×日)將海鮮送達(dá),則銷(xiāo)售商一次性支付給水產(chǎn)養(yǎng)殖基地![]() 萬(wàn)元;若在約定日期前送到,每提前一天銷(xiāo)售商將多支付給水產(chǎn)養(yǎng)殖基地
萬(wàn)元;若在約定日期前送到,每提前一天銷(xiāo)售商將多支付給水產(chǎn)養(yǎng)殖基地![]() 萬(wàn)元;若在約定日期后送到,每遲到一天銷(xiāo)售商將少支付給水產(chǎn)養(yǎng)殖基地
萬(wàn)元;若在約定日期后送到,每遲到一天銷(xiāo)售商將少支付給水產(chǎn)養(yǎng)殖基地![]() 萬(wàn)元.為保證海鮮新鮮度,汽車(chē)只能在約定日期的前兩天出發(fā),且只能選擇其中的一條公路運(yùn)送海鮮,已知下表內(nèi)的信息:
萬(wàn)元.為保證海鮮新鮮度,汽車(chē)只能在約定日期的前兩天出發(fā),且只能選擇其中的一條公路運(yùn)送海鮮,已知下表內(nèi)的信息:
汽車(chē) 行駛路線(xiàn) | 不堵車(chē)的情況下到達(dá)城市乙所需時(shí)間(天) | 堵車(chē)的情況下到達(dá)城市乙所需時(shí)間(天) | 堵車(chē)的概率 | 運(yùn)費(fèi)(萬(wàn)元) |
公路 |
|
|
|
|
公路 |
|
|
|
|
(注:毛利潤(rùn)![]() 銷(xiāo)售商支付給水產(chǎn)養(yǎng)殖基地的費(fèi)用
銷(xiāo)售商支付給水產(chǎn)養(yǎng)殖基地的費(fèi)用![]() 運(yùn)費(fèi))
運(yùn)費(fèi))
(Ⅰ)記汽車(chē)走公路![]() 時(shí)水產(chǎn)養(yǎng)殖基地獲得的毛利潤(rùn)為
時(shí)水產(chǎn)養(yǎng)殖基地獲得的毛利潤(rùn)為![]() (單位:萬(wàn)元),求
(單位:萬(wàn)元),求![]() 的分布列和數(shù)學(xué)期望
的分布列和數(shù)學(xué)期望![]() .
.
(Ⅱ)假設(shè)你是水產(chǎn)養(yǎng)殖基地的決策者,你選擇哪條公路運(yùn)送海鮮有可能讓水產(chǎn)養(yǎng)殖基地獲得的毛利潤(rùn)更多?
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】在直角坐標(biāo)系xOy中,以O為極點(diǎn),x軸正半軸為極軸建立極坐標(biāo)系,圓C的極坐標(biāo)方程為ρ=2![]() cos
cos![]() ,直線(xiàn)l的參數(shù)方程為
,直線(xiàn)l的參數(shù)方程為![]() (t為參數(shù)),直線(xiàn)l與圓C交于A,B兩點(diǎn),P是圓C上不同于A,B的任意一點(diǎn).
(t為參數(shù)),直線(xiàn)l與圓C交于A,B兩點(diǎn),P是圓C上不同于A,B的任意一點(diǎn).
(1)求圓心的極坐標(biāo);
(2)求△PAB面積的最大值.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話(huà):027-86699610 舉報(bào)郵箱:58377363@163.com