
【題目】已知函數![]() (
(![]() ),
),![]() .
.
(1)若對任意的![]() ,
,![]() ,都有
,都有![]() 恒成立,試求m的取值范圍;
恒成立,試求m的取值范圍;
(2)用![]() 表示m,n中的最小值,設函數
表示m,n中的最小值,設函數![]() (
(![]() ),討論關于x的方程
),討論關于x的方程![]() 的實數解的個數.
的實數解的個數.
【答案】(1)![]() ;(2)見解析.
;(2)見解析.
【解析】
(1)根據![]() 恒成立轉化為
恒成立轉化為![]() 恒成立,即來研究函數
恒成立,即來研究函數![]() 的最值,再分當
的最值,再分當![]() ,
,![]() ,
,![]() 時三種情況分分類討論求解.
時三種情況分分類討論求解.
(2) 將方程![]() 的實數解的個數,轉化為函數
的實數解的個數,轉化為函數![]() 零點的個數問題來研究,根據函數
零點的個數問題來研究,根據函數![]() 的定義,分
的定義,分![]() ,
,![]() ,
,![]() ,即
,即![]() ,
,![]() ,
,![]() 三種情況下,對
三種情況下,對![]() 討論.
討論.
(1)![]() ,
,
當![]() ,即
,即![]() 時,
時,![]() 在
在![]() 上單調遞增,
上單調遞增,
![]() ,
,![]() ,
,
所以![]() ,
,
解得![]() ,不合題意舍去,
,不合題意舍去,
當![]() 時,
時,![]() 在
在![]() 上單調遞減,在
上單調遞減,在![]() 上單調遞增,
上單調遞增,
![]() ,
,![]() ,
,
而![]() ,
,![]() ,
,
所以有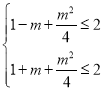 ,
,
解得![]() ,即
,即![]() ,
,
當![]() 即
即![]() 時,
時,![]() 在
在![]() 上單調遞減,
上單調遞減,
![]() ,
,![]() ,
,
![]() ,
,
解得![]() ,不合題意,
,不合題意,
.綜上所述,m的取值范圍為![]() .
.
(2)方程![]() 的實數解的個數
的實數解的個數![]() 函數
函數![]() 零點的個數.
零點的個數.
①當![]() 時,
時,![]() ,所以
,所以![]() ,
,
所以函數![]() 在
在![]() 上沒有零點,即方程
上沒有零點,即方程![]() 在
在![]() 上沒有實數解;
上沒有實數解;
②當![]() 時,
時,![]() ,
,![]() ,
,
若![]() ,即
,即![]() 時,
時,
![]() ,所以
,所以![]() 是函數
是函數![]() 的零點,
的零點,
即方程![]() 有一實數解
有一實數解![]() ,
,
若![]() ,即
,即![]() ,
,
![]() ,所以
,所以![]() 此時不是函數
此時不是函數![]() 的零點,
的零點,
即方程![]() 此時無實數解;
此時無實數解;
.③當![]() 時,
時,![]() ,所以只需考慮
,所以只需考慮![]() 在
在![]() 上的零點個數,
上的零點個數,
則由![]() 得
得![]() ,
,![]() 即問題等價于直線
即問題等價于直線![]() 與函數
與函數![]() ,
,![]() 圖象的交點的個數.
圖象的交點的個數.
由于對勾函數![]() 在
在![]() 上單調遞減,在
上單調遞減,在![]() 上單調遞增,
上單調遞增,
結合![]() ,
,![]() 的圖象可知,
的圖象可知,
當![]() 時,
時,![]() 與函數
與函數![]() ,
,![]() 的圖象沒有交點,
的圖象沒有交點,
即函數![]() 在
在![]() 上沒有零點,即方程
上沒有零點,即方程![]() 在
在![]() 上沒有實數解;
上沒有實數解;
當![]() 或
或![]() 時,
時,![]() 在
在![]() 上有一個實數解;
上有一個實數解;
當![]() 時,
時,![]() 在
在![]() 上有兩個實數解;
上有兩個實數解;
綜上所述,當![]() 或
或![]() 時,方程
時,方程![]() 有一個實數解,
有一個實數解,
當![]() 或
或![]() 時,方程
時,方程![]() 在
在![]() 上有兩個實數解,
上有兩個實數解,
當![]() 時,方程
時,方程![]() 在
在![]() 上有三個實數解.
上有三個實數解.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】某中學的高二(1)班男同學有45名,女同學有15名,老師按照分層抽樣的方法組建了一個4人的課外興趣小組.
(1)求課外興趣小組中男、女同學的人數;
(2)經過一個月的學習、討論,這個興趣小組決定選出兩名同學做某項實驗,方法是先從小組里選出1名同學做實驗,該同學做完后,再從小組內剩下的同學中選一名同學做實驗,求選出的兩名同學中恰有一名女同學的概率;
(3)試驗結束后,第一次做試驗的同學得到的試驗數據為68,70,71,72,74,第二次做試驗的同學得到的試驗數據為69,70,70,72,74 ,請問哪位同學的實驗更穩定?并說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】“雙十一”期間,某淘寶店主對其商品的上架時間![]() (小時)和銷售量
(小時)和銷售量![]() (件)的關系作了統計,得到了如下數據并研究.
(件)的關系作了統計,得到了如下數據并研究.
上架時間 | 2 | 4 | 6 | 8 | 10 | 12 |
銷售量 | 64 | 138 | 205 | 285 | 360 | 430 |
(1)求表中銷售量![]() 的平均數和中位數;
的平均數和中位數;
(2)① 作出散點圖,并判斷變量![]() 與
與![]() 是否線性相關?若研究的方案是先根據前5組數據求線性回歸方程,再利用第6組數據進行檢驗,求線性回歸方程
是否線性相關?若研究的方案是先根據前5組數據求線性回歸方程,再利用第6組數據進行檢驗,求線性回歸方程![]() ;
;
②若根據①中線性回歸方程得到商品上架12小時的銷售量的預測值與檢測值不超過3件,則認為得到的線性回歸方程是理想的,試問:①中的線性回歸方程是否理想.
附:線性回歸方程![]() 中,
中, 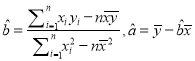 .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某單位有員工1000名,平均每人每年創造利潤10萬元.為增加企業競爭力,決定優化產業結構,調整出![]() 名員工從事第三產業,調整后平均每人每年創造利潤為
名員工從事第三產業,調整后平均每人每年創造利潤為![]() 萬元
萬元![]() ,剩下的員工平均每人每年創造的利潤可以提高
,剩下的員工平均每人每年創造的利潤可以提高![]() .
.
(1)若要保證剩余員工創造的年總利潤不低于原來1000名員工創造的年總利潤,則最多調整出多少名員工從事第三產業?
(2)若要保證剩余員工創造的年總利潤不低于原來1000名員工創造的年總利潤條件下,若要求調整出的員工創造出的年總利潤始終不高于剩余員工創造的年總利潤,則![]() 的取值范圍是多少?
的取值范圍是多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了保護環境,某工廠在政府部門的支持下,進行技術改進:把二氧化碳轉化為某種化工產品,經測算,該處理成本y(萬元)與處理量x(噸)之間的函數關系可近似地表示為: ,且每處理一噸二氧化碳可得價值為20萬元的某種化工產品.
,且每處理一噸二氧化碳可得價值為20萬元的某種化工產品.
(1)當![]() 時,判斷該技術改進能否獲利?如果能獲利,求出最大利潤;如果不能獲利,則國家至少需要補貼多少萬元,該工廠才不虧損?
時,判斷該技術改進能否獲利?如果能獲利,求出最大利潤;如果不能獲利,則國家至少需要補貼多少萬元,該工廠才不虧損?
(2)當處理量為多少噸時,每噸的平均處理成本最少.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設命題![]() 對任意實數
對任意實數![]() ,不等式
,不等式![]() 恒成立;命題
恒成立;命題![]() 方程
方程![]() 表示焦點在
表示焦點在![]() 軸上的雙曲線.
軸上的雙曲線.
(1)若命題![]() 為真命題,求實數
為真命題,求實數![]() 的取值范圍;
的取值范圍;
(2)若命題:“![]() ”為真命題,且“
”為真命題,且“![]() ”為假命題,求實數
”為假命題,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】![]() 九章算術
九章算術![]() 中將底面為長方形,且有一條側棱與底面垂直的四棱錐稱之為“陽馬”
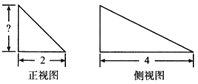
中將底面為長方形,且有一條側棱與底面垂直的四棱錐稱之為“陽馬”![]() 現有一陽馬,其正視圖和側視圖是如圖所示的直角三角形
現有一陽馬,其正視圖和側視圖是如圖所示的直角三角形![]() 若該陽馬的頂點都在同一個球面上,且該球的表面積為
若該陽馬的頂點都在同一個球面上,且該球的表面積為![]() ,則該“陽馬”的體積為__.
,則該“陽馬”的體積為__.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,![]() 、
、![]() 是兩個小區所在地,
是兩個小區所在地,![]() 、
、![]() 到一條公路
到一條公路![]() 的垂直距離分別為
的垂直距離分別為![]()
![]() ,
,![]()
![]() ,
,![]() 兩端之間的距離為
兩端之間的距離為![]()
![]() .
.
(1)某移動公司將在![]() 之間找一點
之間找一點![]() ,在
,在![]() 處建造一個信號塔,使得
處建造一個信號塔,使得![]() 對
對![]() 、
、![]() 的張角與
的張角與![]() 對
對![]() 、
、![]() 的張角相等,試確定點
的張角相等,試確定點![]() 的位置.
的位置.
(2)環保部門將在![]() 之間找一點
之間找一點![]() ,在
,在![]() 處建造一個垃圾處理廠,使得
處建造一個垃圾處理廠,使得![]() 對
對![]() 、
、![]() 所張角最大,試確定點
所張角最大,試確定點![]() 的位置.
的位置.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com