
已知函數![]() 的定義域為
的定義域為![]() 且
且![]() ,對任意
,對任意![]() 都有
都有![]()
![]()
數列![]() 滿足
滿足![]() N
N![]() .證明函數
.證明函數![]() 是奇函數;求數列
是奇函數;求數列![]() 的通項公式;令
的通項公式;令![]() N
N![]() , 證明:當
, 證明:當![]() 時,
時,![]() .
.
(本小題主要考查函數、數列、不等式等知識, 考查化歸與轉化、分類與整合的數學思想方法,以及抽象概括能力、推理論證能力、運算求解能力和創新意識)
【解析】(1)由于對任意![]() ,都有
,都有![]() ,
,
令![]() ,得
,得![]() ,解得
,解得![]() . …… 1分
. …… 1分
令![]() ,得
,得![]() ,∵
,∵![]() ,
,
∴![]() ,即
,即![]() .…… 2分 ∴函數
.…… 2分 ∴函數![]() 是奇函數. …… 3分
是奇函數. …… 3分
(2)解:先用數學歸納法證明![]() .①當
.①當![]() 時,
時,![]() ,得
,得![]() , 結論成立.
, 結論成立.
②假設![]() 時, 結論成立, 即
時, 結論成立, 即![]() ,當
,當![]() 時, 由于
時, 由于![]() ,
, ![]() ,
,
又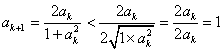 .∴
.∴![]() .即
.即![]() 時, 結論也成立.
時, 結論也成立.
由①②知對任意![]() N
N![]() ,
, ![]() .…… 4分
.…… 4分
求數列![]() 的通項公式提供下面兩種方法.
的通項公式提供下面兩種方法.
法1: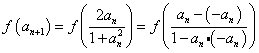
![]() .…………… 5分
.…………… 5分
∵函數![]() 是奇函數, ∴
是奇函數, ∴![]() . ∴
. ∴![]()
![]() . …… 6分
. …… 6分
∴數列![]() 是首項為
是首項為![]() ,公比為
,公比為![]() 的等比數列.
的等比數列.
∴數列![]() 的通項公式為
的通項公式為![]() . ……… 7分
. ……… 7分
法2: ∵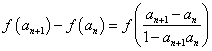 …… 5分
…… 5分
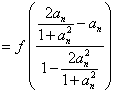
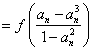
![]()
![]() , ∴
, ∴![]()
![]() .… 6分
.… 6分
∴數列![]() 是首項為
是首項為![]() ,公比為
,公比為![]() 的等比數列.
的等比數列.
∴數列![]() 的通項公式為
的通項公式為![]() .………… 7分
.………… 7分
(3)證法1:由(2)知![]() ,∵
,∵![]()
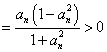 ,
,
∴![]() . … 8分∴
. … 8分∴![]() N
N![]() ,且
,且![]()
∴![]() N
N![]() ,且
,且![]() .… 9分當
.… 9分當![]() 且
且![]() N
N![]() 時,
時,
![]()
![]() …… 10分
…… 10分
![]() …… 11分
…… 11分 ![]()
![]() .
.
∴![]() . … 12分∵
. … 12分∵![]() ,∴當
,∴當![]() 時,
時,![]() .… 13分
.… 13分
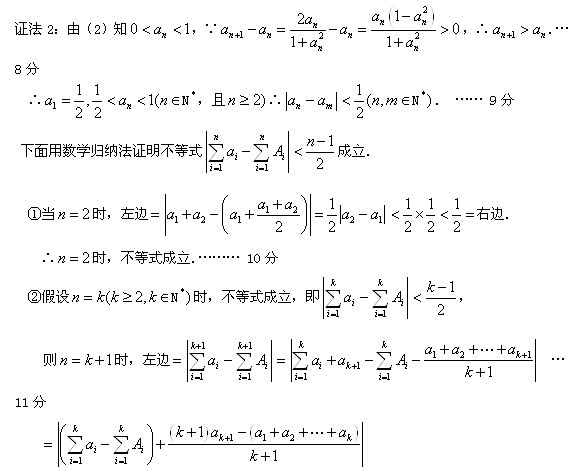 ∴當
∴當![]() 時,
時,![]() . 14分
. 14分
![]() ………… 12分
………… 12分
![]()
![]()
![]()
![]()
![]()
![]()
![]() 右邊.……… 13 ∴
右邊.……… 13 ∴![]() 時,不等式也成立.
時,不等式也成立.
由①②知,當![]() 時,
時,![]() 成立.………… 14分
成立.………… 14分
證法3:由(2)知![]() ,故對
,故對![]() ,有
,有
![]() .… 8分
.… 8分



科目:高中數學 來源:2015屆云南省高二上學期期中考試理科數學試卷(解析版) 題型:選擇題
已知函數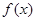 的定義域為
的定義域為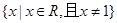 , 且
, 且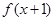 奇函數.當
奇函數.當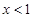 時,
時, 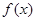 =
=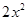 -
-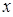 -1,那么函數
-1,那么函數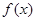 ,當
,當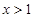 時,
時,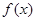 的遞減區間是 ( )
的遞減區間是 ( )
A. B.
B.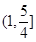 C.
C.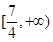 D.
D.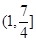
查看答案和解析>>
科目:高中數學 來源:2015屆云南省高二上學期期中考試文科數學試卷(解析版) 題型:選擇題
已知函數 的定義域為
的定義域為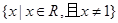 , 且
, 且 奇函數.當
奇函數.當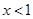 時,
時,  =
=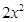 -
-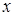 -1,那么函數
-1,那么函數 ,當
,當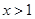 時,
時,  的遞減區間是 ( )
的遞減區間是 ( )
A.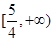 B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中數學 來源:2014屆山東省日照市高三上學期第一次月考理科數學試卷(解析版) 題型:選擇題
已知函數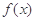 的定義域為
的定義域為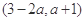 ,且
,且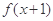 為偶函數,則實數
為偶函數,則實數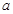 的值可以是( )
的值可以是( )
A.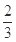 B.
B.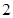 C.
C.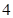 D.
D.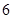
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com