Question

函數f（x）=x³-3tx+m（x∈R，m和t為常數）是奇函數．
（1）求實數m的值和函數f（x）的圖象與橫軸的交點坐標；
（2）設g（x）=|f（x）|（x∈[-1，1]），求g（x）的最大值F（t）；
（3）求F（t）的最小值．

Answer 1

分析：（1）先根據奇函數的性質求出m的值，然后結合函數的單調性，令f（x）=0即可求出x的值，從而求出與x軸的交點坐標．
（2）g（x）=|x³-3xt|（x∈[0，1]）是偶函數，所以只要求出g（x）=|x³-3xt|（x∈[0，1]）的最大值即可．
（3）F（t）在（-∞，

1

4

）上為減函數，

在[ 1 4 ，+∞)為增函數

，所以t=

1

4

時，F（t）取得最小值．

解答：解：（1）由于f（x）為奇函數，易得m=0…（1分）
設f（x）=x³-3tx=x（x²-3t）=0
①當3t＜0時，上述方程只有一個實數根x=0，所以f（x）與x軸的交點坐標為（0，0）
②當3t=0時，上述方程有三個相等實數根x=0，所以f（x）與x軸的交點坐標為（0，0）
③當3t＞0時，上述方程的解為x₁=0，x_2，3=±

3t

，所以f（x）與橫軸的交點坐標分別為：（0，0），（

3t

，0)，(-

3t

，0）…（4分）（少一種情況扣1分）
（2）顯然g（x）=|x³-3xt|（x∈[0，1]）是偶函數，
所以只要求出g（x）=|x³-3xt|（x∈[0，1]）的最大值即可．又f'（x）=3（x²-t）
①t≤0時，則在[0，1]上f（x）為增函數，∴f（x）≥f（0）=0∴f（x）=g（x），故F（t）=f（1）=1-3t…（6分）
②t＞0時，則在[0，1]上f'（x）=3（x+

t

)(x-

t

）
（i）

t

≥1即t≥1時，則在[0，1]上f（x）為減函數∴f（x）≤f（0）=0，

&∴g(x)=-f(x)，

故F（t）=-f（1）=3t-1…（8分）
（ii）0＜t＜1時，則在[0，1]上f'（x）=3（x+

t

)(x-

t

）

x	0	（0， t ）	t	（ t ，1）	1
f'（x）		-	0	+
f（x）	0	↓	極小值-2t t	↑	1-3t

所以可以畫出g（x）的草圖如下，并且由圖可知：

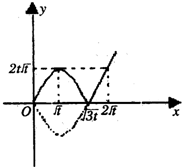
（1⁰）當

t

＜1≤2

t

即

1

4

≤t＜1時，g(x)的最大值F(t)=-f(

t

)=2t

t

（2⁰）當1＞2

t

即0＜t＜

1

4

時，g（x）的最大值F（t）=f（1）=1-3t…（10分）
綜上所述：F（t）=

1-3t(t＜ 1 4 ) 2t t ( 1 4 ≤t＜1) 3t-1(t≥1)

…（12分）
（3）顯然F（t）在（-∞，

1

4

）上為減函數，

在[ 1 4 ，+∞)為增函數

∴F（t）的最小值=F（

1

4

)=

1

4

．

點評：本題主要考查了三次函數的奇偶性，單調性等有關知識，考查了利用導數研究函數的最值，屬于基礎題．