
【題目】在非負數構成的![]() 數表
數表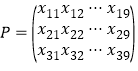 中,每行的數互不相同,前六列中每列的三數之和為1,
中,每行的數互不相同,前六列中每列的三數之和為1,![]() 均大于1.如果
均大于1.如果![]() 的前三列構成的數表
的前三列構成的數表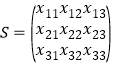 滿足下面的性質
滿足下面的性質![]() :對于數表
:對于數表![]() 中的任意一列
中的任意一列![]() (
(![]() )均存在某個
)均存在某個![]() 使得
使得![]() .①
.①
求證:(1)最小值![]() (
(![]() )一定去自數表
)一定去自數表![]() 的不同列;
的不同列;
(2)存在數表![]() 中唯一的一列
中唯一的一列![]() (
(![]() )使得
)使得![]() 數表
數表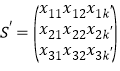 仍然具有性質(
仍然具有性質(![]() ).
).
【答案】見解析
【解析】
(1)假設最小值![]() (
(![]() )不是取自數表的不同列.則存在一列不含任何
)不是取自數表的不同列.則存在一列不含任何![]() 不妨設
不妨設![]() (
(![]() ).由于數表
).由于數表![]() 中同一行中的任何兩個元素都不等,于是,
中同一行中的任何兩個元素都不等,于是,![]() (
(![]() ).使得
).使得![]() .矛盾.
.矛盾.
(2)由抽屜原理知![]() 中至少有兩個值取在同一列.不妨設
中至少有兩個值取在同一列.不妨設![]() .由(1)知數表
.由(1)知數表![]() 的第一列一定含有某個
的第一列一定含有某個![]() ,則只能是
,則只能是![]() .
.
同理,第二列中也必含某個![]() (
(![]() ).不妨設
).不妨設![]() .
.
于是,![]() ,即
,即![]() 是數表
是數表![]() 中的對角線上數字:
中的對角線上數字:![]() .
.
記![]() .令集合
.令集合![]() .顯然,
.顯然,![]() 且
且![]() .因為
.因為![]() ,所以,
,所以,![]() .故
.故![]() .于是,存在
.于是,存在![]() .使得
.使得![]() .顯然,
.顯然,![]() .下面證明:
.下面證明:![]() 數表
數表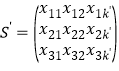 具有性質(
具有性質(![]() ).
).
從上面的選法可知![]() (
(![]() ).這說明
).這說明![]() .
.
又由![]() 滿足性質(
滿足性質(![]() ),在式①中取
),在式①中取![]() ,推得
,推得![]() .于是,
.于是,![]() .接下來證明:對任意的
.接下來證明:對任意的![]() ,存在某個
,存在某個![]() (
(![]() )使得
)使得![]() .
.
假若不然,則![]() (
(![]() )且
)且![]() .這與
.這與![]() 的最大性矛盾.因此,數表
的最大性矛盾.因此,數表![]() 滿足性質(
滿足性質(![]() ).
).
再證唯一性.設有![]() 使得數表
使得數表 具有性質(
具有性質(![]() ).
).
不失一般性,可假定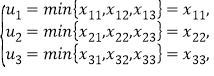 ②
②
![]() .由于
.由于![]() 及(1),有
及(1),有![]() .又由(1)知,或者
.又由(1)知,或者![]() ,③或者
,③或者![]() ④如果式③成立,則
④如果式③成立,則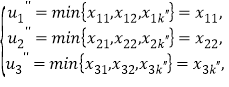 ⑤由數表
⑤由數表![]() 滿足性質(
滿足性質(![]() ),則對于
),則對于![]() 至少存在一個
至少存在一個![]() ,使得
,使得![]() .
.
又由式②、⑤知![]() .所以,只能有
.所以,只能有![]() .同理,由數表
.同理,由數表![]() 滿足性質(
滿足性質(![]() )得
)得![]() .于是,
.于是,![]() ,即數表
,即數表![]() .如果式④成立,則
.如果式④成立,則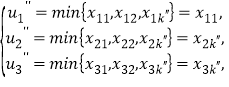 ⑥由數表
⑥由數表![]() 滿足性質(
滿足性質(![]() ),則對于
),則對于![]() ,存在某個
,存在某個![]() (
(![]() )使得
)使得![]() .由
.由![]() 及式②、⑥知
及式②、⑥知![]() .于是,只能有
.于是,只能有![]() .同理,由
.同理,由![]() 滿足性質(
滿足性質(![]() )及
)及![]() 得
得![]() .從而
.從而![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】《九章算術》是我國古代數學文化的優秀遺產,數學家劉徽在注解《九章算術》時,發現當圓內接正多邊行的邊數無限增加時,多邊形的面積可無限逼近圓的面積,為此他創立了割圓術,利用割圓術,劉徽得到了圓周率精確到小數點后四位3.1416,后人稱3.14為徽率,如圖是利用劉徽的割圓術設計的程序框圖,若結束程序時,則輸出的![]() 為( )(
為( )(![]() ,
,![]() ,
,![]() )
)
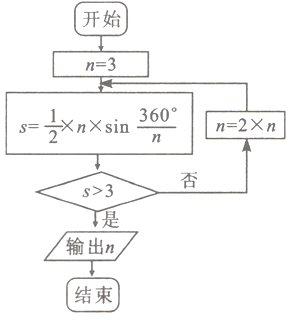
A. 6 B. 12 C. 24 D. 48
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若存在實常數![]() 和
和![]() ,使得函數
,使得函數![]() 和
和![]() 對其公共定義域上的任意實數
對其公共定義域上的任意實數![]() 都滿足:
都滿足:![]() 和
和![]() 恒成立,則稱此直線
恒成立,則稱此直線![]() 為
為![]() 和
和![]() 的“隔離直線”,已知函數
的“隔離直線”,已知函數![]() ,
,![]() ,
,![]() ,下列命題為真命題的是( )
,下列命題為真命題的是( )
A.![]() 在
在![]() 內單調遞減
內單調遞減
B.![]() 和
和![]() 之間存在“隔離直線”,且
之間存在“隔離直線”,且![]() 的最小值為
的最小值為![]()
C.![]() 和
和![]() 之間存在“隔離直線”,且
之間存在“隔離直線”,且![]() 的取值范圍是
的取值范圍是![]()
D.![]() 和
和![]() 之間存在唯一的“隔離直線”
之間存在唯一的“隔離直線”![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】羅馬數字是歐洲在阿拉伯數字傳入之前使用的一種數碼,它的產生標志著一種古代文明的進步.羅馬數字的表示法如下:
數字 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
形式 | Ⅰ | Ⅱ | Ⅲ | Ⅳ | Ⅴ | Ⅵ | Ⅶ | Ⅷ | Ⅸ |
其中“Ⅰ”需要1根火柴,“Ⅴ”與“X”需要2根火柴,若為0,則用空位表示. (如123表示為![]() ,405表示為
,405表示為![]() )如果把6根火柴以適當的方式全部放入下面的表格中,那么可以表示的不同的三位數的個數為( )
)如果把6根火柴以適當的方式全部放入下面的表格中,那么可以表示的不同的三位數的個數為( )
![]()
A.87B.95C.100D.103
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓E的一個頂點為![]() ,焦點在x軸上,若橢圓的右焦點到直線
,焦點在x軸上,若橢圓的右焦點到直線![]() 的距離是3.
的距離是3.
![]() 求橢圓E的方程;
求橢圓E的方程;
![]() 設過點A的直線l與該橢圓交于另一點B,當弦AB的長度最大時,求直線l的方程.
設過點A的直線l與該橢圓交于另一點B,當弦AB的長度最大時,求直線l的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點![]() 是拋物線
是拋物線![]() 的焦點,若點
的焦點,若點![]() 在拋物線
在拋物線![]() 上,且
上,且![]()
![]() 求拋物線
求拋物線![]() 的方程;
的方程;
![]() 動直線
動直線![]() 與拋物線
與拋物線![]() 相交于
相交于![]() 兩點,問:在
兩點,問:在![]() 軸上是否存在定點
軸上是否存在定點![]() 其中
其中![]() ,使得向量
,使得向量![]() 與向量
與向量![]() 共線
共線![]() 其中
其中![]() 為坐標原點
為坐標原點![]() ?若存在,求出點
?若存在,求出點![]() 的坐標;若不存在,請說明理由.
的坐標;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com