
【題目】已知自變量為![]() 的函數(shù)
的函數(shù)![]() .其中
.其中![]() ,
,![]() 為自然對數(shù)的底,
為自然對數(shù)的底,![]() .
.
(Ⅰ)求函數(shù)![]() 與
與![]() 的單調(diào)區(qū)間,并且討論函數(shù)
的單調(diào)區(qū)間,并且討論函數(shù)![]() 的單調(diào)性;
的單調(diào)性;
(Ⅱ)已知![]() ,求證:
,求證:
(ⅰ)方程![]() 有兩個根
有兩個根![]() ,
,![]() ;
;
(ⅱ)若(ⅰ)中的兩個根滿足![]() ,
,![]() ,則
,則![]() ,
,![]() .
.
【答案】(Ⅰ)![]() 增區(qū)間為
增區(qū)間為![]() ,減區(qū)間為
,減區(qū)間為![]() ;
;![]() 增區(qū)間為
增區(qū)間為![]() ,見解析(Ⅱ)(ⅰ)見解析(ⅱ)見解析
,見解析(Ⅱ)(ⅰ)見解析(ⅱ)見解析
【解析】
(Ⅰ)分別求得![]() ,
,![]() 的導(dǎo)數(shù),由導(dǎo)數(shù)大于0,可得增區(qū)間;導(dǎo)數(shù)小于0,可得減區(qū)間,進而得到最值,可得單調(diào)區(qū)間;討論
的導(dǎo)數(shù),由導(dǎo)數(shù)大于0,可得增區(qū)間;導(dǎo)數(shù)小于0,可得減區(qū)間,進而得到最值,可得單調(diào)區(qū)間;討論![]() 為奇數(shù)和偶數(shù),即可得到所求單調(diào)性;
為奇數(shù)和偶數(shù),即可得到所求單調(diào)性;
(Ⅱ)![]() ,(ⅰ)運用
,(ⅰ)運用![]() 為奇數(shù)的函數(shù)的單調(diào)性,結(jié)合圖象即可得證;
為奇數(shù)的函數(shù)的單調(diào)性,結(jié)合圖象即可得證;
(ⅱ)![]() 為奇數(shù)時,
為奇數(shù)時,![]() 在
在![]() 遞減,在
遞減,在![]() 遞增,且
遞增,且![]() 越小,函數(shù)的圖象與直線
越小,函數(shù)的圖象與直線![]() 的交點越靠近
的交點越靠近![]() 軸,即可得證.
軸,即可得證.
解:(Ⅰ)![]() 的導(dǎo)數(shù)為
的導(dǎo)數(shù)為
![]() ,由
,由![]() 時
時![]() ;由
;由![]() 時
時![]() ;
;
可得![]() 的增區(qū)間為
的增區(qū)間為![]() ,減區(qū)間為
,減區(qū)間為![]() ;
;
![]() 的導(dǎo)數(shù)為
的導(dǎo)數(shù)為
![]() ,
,![]() ,
,
可得![]() ,
,
可得![]() 的增區(qū)間為
的增區(qū)間為![]() ;
;
![]() 經(jīng)過
經(jīng)過![]() 次導(dǎo)數(shù)可得
次導(dǎo)數(shù)可得![]() ,
,
由![]() ,在
,在![]() 時,
時,![]() ;
;![]() 時
時![]() ;
;
則![]() 次求導(dǎo)時,導(dǎo)函數(shù)在
次求導(dǎo)時,導(dǎo)函數(shù)在![]() 遞增;
遞增;![]() 遞減,
遞減,
即有導(dǎo)函數(shù)的最小值為0,
可得![]() 為奇數(shù),
為奇數(shù),![]() 在
在![]() 遞減,在
遞減,在![]() 遞增;
遞增;
![]() 為偶數(shù)時,
為偶數(shù)時,![]() 在
在![]() 遞增;
遞增;
(Ⅱ)證明:![]() ,(ⅰ)由
,(ⅰ)由![]() 為奇數(shù),
為奇數(shù),![]() 在
在![]() 遞減,
遞減,
在![]() 遞增;可得
遞增;可得![]() ,有最小值0,無最大值,
,有最小值0,無最大值,
則方程![]() 有兩個根
有兩個根![]() ,
,![]() ;
;
(ⅱ)若(ⅰ)中的兩個根滿足![]() ,
,![]() ,
,
由于![]() 為奇數(shù)時,
為奇數(shù)時,![]() 在
在![]() 遞減,在
遞減,在![]() 遞增,
遞增,
且![]() 越小,函數(shù)的圖象與直線
越小,函數(shù)的圖象與直線![]() 的交點越靠近
的交點越靠近![]() 軸,
軸,
則![]() ,
,![]() .
.


科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在四棱錐![]() 中,平面
中,平面![]() 平面ABCD,
平面ABCD,![]() ,
,![]() ,底面ABCD是邊長為2的菱形,點E,F分別為棱DC,BC的中點,點G是棱SC靠近點C的四等分點.
,底面ABCD是邊長為2的菱形,點E,F分別為棱DC,BC的中點,點G是棱SC靠近點C的四等分點.
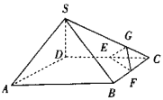
求證:(1)直線![]() 平面EFG;
平面EFG;
(2)直線![]() 平面SDB.
平面SDB.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知雙曲線![]() 的兩頂點分別為
的兩頂點分別為![]() ,
,![]() 為雙曲線的一個焦點,
為雙曲線的一個焦點,![]() 為虛軸的一個端點,若在線段
為虛軸的一個端點,若在線段![]() 上(不含端點)存在兩點
上(不含端點)存在兩點![]() ,使得
,使得![]() ,則雙曲線的漸近線斜率
,則雙曲線的漸近線斜率![]() 的平方的取值范圍是( )
的平方的取值范圍是( )
A.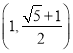 B.
B.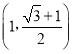 C.
C.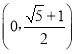 D.
D.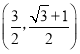
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】隨著時代的發(fā)展和社會的進步,“農(nóng)村淘寶”發(fā)展十分迅速,促進“農(nóng)產(chǎn)品進城”和“消費品下鄉(xiāng)”.“農(nóng)產(chǎn)品進城”很好地解決了農(nóng)產(chǎn)品與市場的對接問題,使農(nóng)民收入逐步提高,生活水平得到改善,農(nóng)村從事網(wǎng)店經(jīng)營的人收入逐步提高.西鳳臍橙是四川省南充市的特產(chǎn),因果實呈橢圓形、色澤橙紅、果面光滑、無核、果肉脆嫩化渣、汁多味濃,深受人們的喜愛.為此小王開網(wǎng)店銷售西鳳臍橙,每月月初購進西鳳臍橙,每售出1噸西鳳臍橙獲利潤800元,未售出的西鳳臍橙,每1噸虧損500元.經(jīng)市場調(diào)研,根據(jù)以往的銷售統(tǒng)計,得到一個月內(nèi)西鳳臍橙市場的需求量的頻率分布直方圖如圖所示.小王為下一個月購進了100噸西鳳臍橙,以x(單位:噸)表示下一個月內(nèi)市場的需求量,y(單位:元)表示下一個月內(nèi)經(jīng)銷西鳳臍橙的銷售利潤.
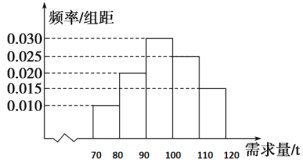
(1)將y表示為x的函數(shù);
(2)根據(jù)頻率分布直方圖估計小王的網(wǎng)店下一個月銷售利潤y不少于67000元的概率;
(3)在直方圖的需求量分組中,以各組的區(qū)間中點值代表該組的各個值,需求量落入該區(qū)間的頻率作為需求量取該區(qū)間中點值的概率,(例如:若需求量![]() ,則取
,則取![]() ,且
,且![]() 的概率等于需求量落入
的概率等于需求量落入![]() 的頻率),求小王的網(wǎng)店下一個月銷售利潤y的分布列和數(shù)學(xué)期望.
的頻率),求小王的網(wǎng)店下一個月銷售利潤y的分布列和數(shù)學(xué)期望.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在正四面體 ABCD 中,P,Q分別是棱 AB,CD的中點,E,F(xiàn)分別是直線AB,CD上的動點,M 是EF 的中點,則能使點 M 的軌跡是圓的條件是( )
A. PE+QF=2B. PEQF=2
C. PE=2QFD. PE2+QF2=2
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在四棱錐![]() 的底面
的底面![]() 中,
中,![]() ∥
∥![]() ,
,![]() ,
,![]() 平面
平面![]() ,
,![]() 是
是![]() 的中點,且
的中點,且![]()
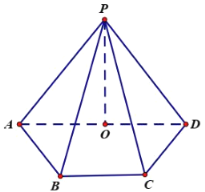
(1)求證:![]() ∥平面
∥平面![]() ;
;
(2)求二面角![]() 的余弦值;
的余弦值;
(3)在線段![]() 內(nèi)是否存在點
內(nèi)是否存在點![]() ,使得
,使得![]() ?若存在指出點
?若存在指出點![]() 的位置,若不存在,請說明理由.
的位置,若不存在,請說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() 的導(dǎo)函數(shù)為
的導(dǎo)函數(shù)為![]() ,且對任意的實數(shù)x都有
,且對任意的實數(shù)x都有![]() (e是自然對數(shù)的底數(shù)),且
(e是自然對數(shù)的底數(shù)),且![]() ,若關(guān)于x的不等式
,若關(guān)于x的不等式![]() 的解集中恰有兩個整數(shù),則實數(shù)m的取值范圍是( )
的解集中恰有兩個整數(shù),則實數(shù)m的取值范圍是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓![]() 的左、右焦點分別為
的左、右焦點分別為![]() ,離心率為
,離心率為![]() ,
,![]() 為橢圓上一動點(異于左右頂點),
為橢圓上一動點(異于左右頂點),![]() 面積的最大值為
面積的最大值為![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)若直線![]() 與橢圓
與橢圓![]() 相交于點
相交于點![]() 兩點,問
兩點,問![]() 軸上是否存在點
軸上是否存在點![]() ,使得
,使得![]() 是以
是以![]() 為直角頂點的等腰直角三角形?若存在,求點
為直角頂點的等腰直角三角形?若存在,求點![]() 的坐標;若不存在,請說明理由.
的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,已知多面體![]() 的底面
的底面![]() 是邊長為
是邊長為![]() 的菱形,
的菱形, ![]()
![]() 底面
底面![]() ,
, ![]() ,且
,且![]() .
.
(1)證明:平面![]() 平面
平面![]() ;
;
(2)若直線![]() 與平面
與平面![]() 所成的角為
所成的角為![]() ,求二面角
,求二面角
![]() 的余弦值.
的余弦值.

查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com