【題目】過點
作圓
的切線
，已知
，
分別為切點，直線
恰好經過橢圓的右焦點和下頂點，則直線方程為___________；橢圓的標準方程是__________．
【答案】
【解析】
①當過點
的直線
斜率不存在時，直線方程為
，切點的坐標
；
②當直線斜率存在時，設方程為
，根據圓心
到切線的距離等于半徑
，求出
確定直線方程，直線方程與圓方程的聯立，進一步求出切點的坐標
，再求出
方程，則橢圓的右焦點及下頂點可求，其標準方程可求.
解：①當過點的直線斜率不存在時，直線方程為，切點的坐標；
②當直線斜率存在時，設方程為，即
，
根據直線與圓相切，圓心到切線的距離等于半徑，得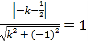
可以得到切線斜率，即
直線方程與圓方程的聯立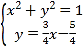
可以得切點的坐標，
根據
、
兩點坐標可以得到直線方程為，（或利用過圓
上一點
作圓的兩條切線，則過兩切點的直線方程為
）
依題意，與
軸的交點
即為橢圓右焦點，得
，
與
軸的交點
即為橢圓下頂點坐標，所以
，
根據公式得
，
因此，橢圓方程為．
世紀百通期末金卷系列答案科目：高中數學 來源： 題型：
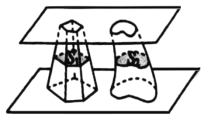
【題目】南北朝時代的偉大科學家祖暅在數學上有突出貢獻，他在實踐的基礎上提出祖暅原理：“冪勢既同，則積不容異”．其含義是：夾在兩個平行平面之間的兩個幾何體，被平行于這兩個平行平面的任意平面所截，如果截得的兩個截面的面積總相等，那么這兩個幾何體的體積相等，如圖，夾在兩個平行平面之間的兩個幾何體的體積分別為
，
，被平行于這兩個平面的任意平面截得的兩個截面面積分別為
、
，則“、不總相等”是“，不相等”的（ ）
A.充分而不必要條件B.必要而不充分條件
C.充分必要條件D.既不充分也不必要條件
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】高斯是德國著名的數學家，近代數學奠基者之一，享有“數學王子”的稱號，用其名字命名的“高斯函數”為：設
，用
表示不超過
的最大整數，則
稱為高斯函數，例如：
，
．已知函數
，函數
，則下列命題中真命題的個數是（ ）
①
圖象關于
對稱；
②
是奇函數；
③在
上是增函數；
④的值域是
.
A.
B.
C.
D.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】對某兩名高三學生在連續9次數學測試中的成績（單位：分）進行統計得到折線圖，下面是關于這兩位同學的數學成績分析．
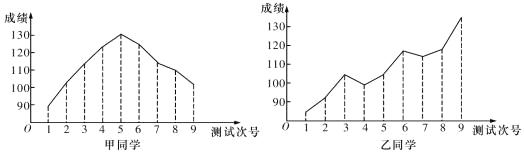
①甲同學的成績折線圖具有較好的對稱性，故平均成績為130分；
②根據甲同學成績折線圖提供的數據進行統計，估計該同學平均成績在區間
內；
③乙同學的數學成績與測試次號具有比較明顯的線性相關性，且為正相關；
④乙同學連續九次測驗成績每一次均有明顯進步．
其中正確的個數為（ ）
A.
B.
C.
D.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓
的焦距為2，過點
.
（1）求橢圓
的標準方程；
（2）設橢圓的右焦點為F，定點
，過點F且斜率不為零的直線l與橢圓交于A，B兩點，以線段AP為直徑的圓與直線
的另一個交點為Q，證明：直線BQ恒過一定點，并求出該定點的坐標.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知點F1、F2分別為雙曲線C：
（a＞0，b＞0）的左、右焦點，點M（x0，y0）（x0＜0）為C的漸近線與圓x2+y2＝a2的一個交點，O為坐標原點，若直線F1M與C的右支交于點N，且|MN|＝|NF2|+|OF2|，則雙曲線C的離心率為_____．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
