
如圖1,![]() 、
、![]() 是橢圓
是橢圓![]() 的長軸上兩點,
的長軸上兩點,![]() 分別為橢圓的短軸和長軸的端點,
分別為橢圓的短軸和長軸的端點,![]() 是
是![]() 上的動點,若
上的動點,若![]() 的最大值與最小值分別為3、
的最大值與最小值分別為3、![]() .
.
(1)求橢圓的離心率;
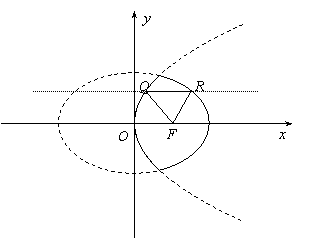
(2)如圖2,點F(1,0),動點Q、R分別在拋物線![]() 及橢圓
及橢圓![]() 的實線部分上運動,且QR∥x軸,求△FQR的周長l的取值范圍.
的實線部分上運動,且QR∥x軸,求△FQR的周長l的取值范圍.
 | |||
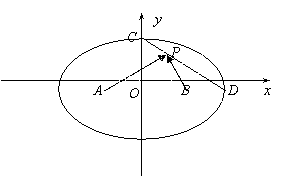 | |||
(圖1) (圖2)
(1)設![]() ,則
,則![]()
∴![]() , ………… 2分
, ………… 2分
∵![]() 的最大值與最小值分別為3、
的最大值與最小值分別為3、![]() ,
,
∴ ![]() 的最大值與最小值分別為4、
的最大值與最小值分別為4、![]() , ………… 3分
, ………… 3分
而![]() 表示線段CD上的點到原點的距離OP的平方
表示線段CD上的點到原點的距離OP的平方
∴點OP的最大值為OD =2,即![]() ………… 5分
………… 5分
OP的最小值即為O到線段CD的距離![]() ,
,
由平面幾何知識得OC=![]() ,即
,即![]() ,…………7分
,…………7分
得![]() ,則橢圓的離心率
,則橢圓的離心率![]()
![]() . ………… 9分
. ………… 9分
(2)設![]() ,由拋物線的定義知
,由拋物線的定義知![]() 等于點
等于點![]() 到拋物線準線
到拋物線準線![]() 的距離,
的距離,
∴![]() 等于點
等于點![]() 到拋物線準線
到拋物線準線![]() 的距離為
的距離為![]() ………… 11分
………… 11分
由橢圓的第二定義知![]() ,
,
∴△NAB的周長l=![]()
![]() =
=![]() .………… 13分
.………… 13分
由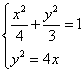 得:拋物線與橢圓交點的橫坐標為
得:拋物線與橢圓交點的橫坐標為![]() ,即得
,即得![]() .
.
所以△FQR的周長l的取值范圍為![]() .………… 16分
.………… 16分


 寒假天地重慶出版社系列答案
寒假天地重慶出版社系列答案科目:高中數學 來源: 題型:
 (2008•湖北模擬)如圖,設F是橢圓
(2008•湖北模擬)如圖,設F是橢圓| x2 |
| a2 |
| y2 |
| b2 |
查看答案和解析>>
科目:高中數學 來源:2012江蘇高考數學填空題提升練習(14) 題型:022
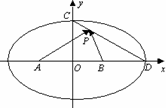
如圖,已知A(-1,0)、B(1,0)是橢圓![]() 的長軸上兩定點,C,D分別為橢圓的短軸和長軸的端點,P是線段CD上的動點,若
的長軸上兩定點,C,D分別為橢圓的短軸和長軸的端點,P是線段CD上的動點,若![]() 的最大值與最小值分別為3、
的最大值與最小值分別為3、![]() ,則橢圓方程為________.
,則橢圓方程為________.
查看答案和解析>>
科目:高中數學 來源:重慶市萬州二中2011屆高三3月月考數學理科試題 題型:044
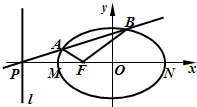
如圖,設F是橢圓![]() 的左焦點,直線l為對應的準線,直線l與x軸交于P點,MN為橢圓的長軸,已知|MN|=8,且|PM|=2|MF|.
的左焦點,直線l為對應的準線,直線l與x軸交于P點,MN為橢圓的長軸,已知|MN|=8,且|PM|=2|MF|.
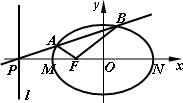
(1)求橢圓的標準方程;
(2)求證:對于任意的割線PAB,恒有![]() ;
;
(3)求三角形△ABF面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
(13分)如圖,設F是橢圓![]() 的左焦點,直線l為其左準線,直線l與x軸交于點P,線段MN為橢圓的長軸,已知
的左焦點,直線l為其左準線,直線l與x軸交于點P,線段MN為橢圓的長軸,已知
![]()
(1)求橢圓C的標準方程;
(2)若過點P的直線與橢圓相交于不同兩點A、B求證:∠AFM=∠BFN;
(3)求三角形ABF面積的最大值。查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com