
(本題滿(mǎn)分12分)
如圖所示的幾何體是由以正三角形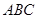 為底面的直棱柱被平面
為底面的直棱柱被平面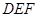 所截而得.
所截而得. 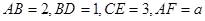 ,
, 為
為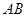 的中點(diǎn).
的中點(diǎn).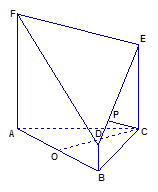
(1)當(dāng)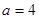 時(shí),求平面
時(shí),求平面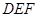 與平面
與平面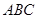 的夾角的余弦值;
的夾角的余弦值;
(2)當(dāng) 為何值時(shí),在棱
為何值時(shí),在棱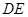 上存在點(diǎn)
上存在點(diǎn) ,使
,使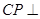 平面
平面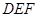 ?
?
(1) (2)2
(2)2
解析試題分析:(1)分別取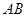 、
、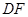 的中點(diǎn)
的中點(diǎn) 、
、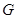 ,連接
,連接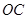 、
、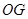 .
.
以直線(xiàn)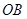 、
、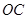 、
、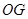 分別為
分別為 軸、
軸、 軸、
軸、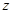 軸建立如圖所示的空間直角坐標(biāo)系,
軸建立如圖所示的空間直角坐標(biāo)系,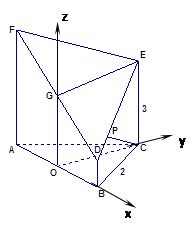
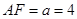 ,則
,則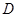 、
、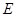 、
、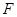 的坐標(biāo)分別為
的坐標(biāo)分別為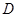 (1,0,1)、
(1,0,1)、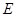 (0,
(0,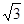 ,3)、
,3)、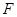 (-1,0,4),
(-1,0,4),
∴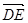 =(-1,
=(-1,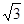 ,2),
,2),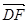 =(-2,0,3)
=(-2,0,3)
設(shè)平面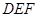 的法向量
的法向量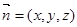 ,
,
由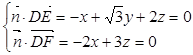 得
得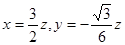 ,可取
,可取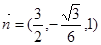 …… 3分
…… 3分
平面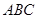 的法向量可以取
的法向量可以取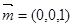
∴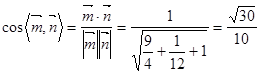 …… 5分
…… 5分
∴平面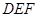 與平面
與平面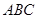 的夾角的余弦值為
的夾角的余弦值為 . ……6分
. ……6分
(2)在(1)的坐標(biāo)系中,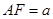 ,
,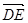 =(-1,
=(-1,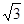 ,2),
,2),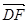 =(-2,0,
=(-2,0, -1).
-1).
因 在
在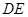 上,設(shè)
上,設(shè)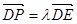 ,則
,則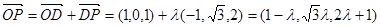
∴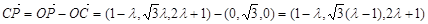
于是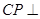 平面
平面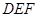 的充要條件為
的充要條件為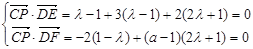
由此解得,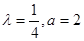 ……10分
……10分
即當(dāng) =2時(shí),在
=2時(shí),在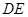 上存在靠近
上存在靠近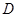 的第一個(gè)四等分點(diǎn)
的第一個(gè)四等分點(diǎn) ,使
,使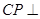 平面
平面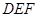 . ……12分
. ……12分
考點(diǎn):空間向量求解二面角,判定線(xiàn)面垂直
點(diǎn)評(píng):空間向量解決立體幾何問(wèn)題的關(guān)鍵是建立合適的坐標(biāo)系,找準(zhǔn)相關(guān)點(diǎn)的坐標(biāo)


 閱讀快車(chē)系列答案
閱讀快車(chē)系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
如圖,在四棱錐 中,底面ABCD是一直角梯形,
中,底面ABCD是一直角梯形,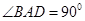 ,
,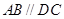 ,
, ,且PA=AD=DC=
,且PA=AD=DC=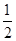 AB=1.
AB=1.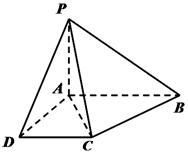
(1)證明:平面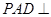 平面
平面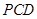
(2)設(shè)AB,PA,BC的中點(diǎn)依次為M、N、T,求證:PB∥平面MNT
(3)求異面直線(xiàn) 與
與 所成角的余弦值
所成角的余弦值
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
(本題13分)
如圖,在四棱錐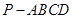 中,
中,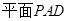
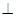 平面
平面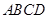 ,底面
,底面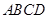 是菱形,
是菱形,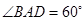 .
.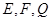 分別是
分別是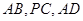 的中點(diǎn).
的中點(diǎn).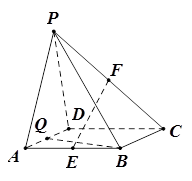
(1) 求證: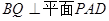 ;
;
(2) 求證: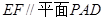 .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
如圖,四棱錐S-ABCD 的底面是正方形,每條側(cè)棱的長(zhǎng)都是底面邊長(zhǎng)的 倍,P為側(cè)棱SD上的點(diǎn).
倍,P為側(cè)棱SD上的點(diǎn).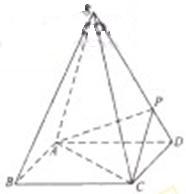
(Ⅰ)求證:AC⊥SD;
(Ⅱ)若SD⊥平面PAC,則側(cè)棱SC上是否存在一點(diǎn)E,使得BE∥平面PAC。若存在,求SE:EC的值;若不存在,試說(shuō)明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
(本小題滿(mǎn)分12分)在幾何體ABCDE中,∠BAC=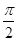 ,DC⊥平面ABC,EB⊥平面ABC,F(xiàn)是BC的中點(diǎn),AB=AC=BE=2,CD=1
,DC⊥平面ABC,EB⊥平面ABC,F(xiàn)是BC的中點(diǎn),AB=AC=BE=2,CD=1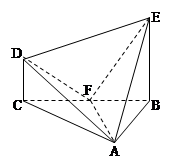
(Ⅰ)求證:DC∥平面ABE;
(Ⅱ)求證:AF⊥平面BCDE;
(Ⅲ)求證:平面AFD⊥平面AFE.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
(本小題滿(mǎn)分14分)
如圖所示,四棱錐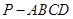 中,底面
中,底面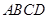 為正方形,
為正方形, 平面
平面 ,
,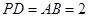 ,
,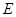 ,
, ,
,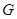 分別為
分別為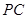 、
、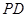 、
、 的中點(diǎn).
的中點(diǎn).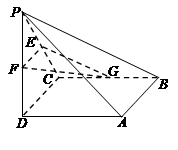
(1)求證: ;
;
(2)求平面EFG與平面ABCD所成銳二面角的余弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
圖形P-ABCD中,底面ABCD是正方形,PA⊥底面ABCD,PA=AB,Q是PC中點(diǎn).AC,BD交于O點(diǎn).
(1)二面角Q-BD-C的大小:
(2)求二面角B-QD-C的大小.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
如圖,四面體ABCD中,O、E分別是BD、BC的中點(diǎn),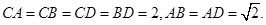
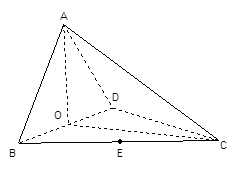
(I)求證: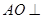 平面BCD;
平面BCD;
(II)求異面直線(xiàn)AB與CD所成角的余弦值;
(III)求點(diǎn)E到平面ACD的距離。
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
(本小題滿(mǎn)分13分)
如圖,在三棱錐S-ABC中,BC⊥平面SAC,AD⊥SC.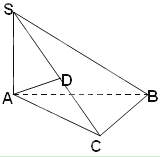
(Ⅰ)求證:AD⊥平面SBC;
(Ⅱ)試在SB上找一點(diǎn)E,使得平面ABS⊥平面ADE,并證明你的結(jié)論.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話(huà):027-86699610 舉報(bào)郵箱:58377363@163.com