精英家教網(wǎng)> 2026年優(yōu)課堂給力A加八年級數(shù)學(xué)上冊北師大版 > 第1頁 參考答案
2026年優(yōu)課堂給力A加八年級數(shù)學(xué)上冊北師大版
注:目前有些書本章節(jié)名稱可能整理的還不是很完善,但都是按照順序排列的,請同學(xué)們按照順序仔細查找。練習(xí)冊2026年優(yōu)課堂給力A加八年級數(shù)學(xué)上冊北師大版答案主要是用來給同學(xué)們做完題方便對答案用的,請勿直接抄襲。
1.勾股定理:直角三角形
。如果用$a$,$b$和$c$分別表示直角三角形的兩直角邊和斜邊,那么
。
2.應(yīng)用勾股定理的注意事項
(1)勾股定理使用的前提是在直角三角形中;
(2)要分清直角邊和斜邊,在$Rt\triangle ABC$中,直角不一定是$\angle C$,也就是$c$不一定是斜邊。
認識勾股定理
答案:兩直角邊的平方和等于斜邊的平方;$a^{2}+b^{2}=c^{2}$
解析:
勾股定理是直角三角形的重要性質(zhì),其內(nèi)容為兩直角邊的平方和等于斜邊的平方。用字母表示時,若兩直角邊為$a$、$b$,斜邊為$c$,則關(guān)系式為$a^{2}+b^{2}=c^{2}$。
【例1】下列說法中正確的是 (
)
A.已知$a$,$b$,$c$是三角
形
的三邊,則$a^{2}+b^{2}=c^{2}$
B.在直角三角形中兩邊和的平方等于第三邊的平方
C.在$Rt\triangle ABC$中,$\angle C = 90^{\circ}$,則$BC^{2}+AC^{2}=AB^{2}$
D.在$Rt\triangle ABC$中,$\angle B = 90^{\circ}$,則$BC^{2}+AC^{2}=AB^{2}$
答案:C
解析:
A. 沒有說明三角形是直角三角形,也沒有說明$c$是斜邊,所以A選項錯誤。
B. 在直角三角形中,必須是兩條直角邊的平方和等于斜邊的平方,而不是兩邊和的平方等于第三邊的平方,所以B選項錯誤。
C. 在$Rt\triangle ABC$中,$\angle C = 90^{\circ}$,根據(jù)勾股定理,兩條直角邊的平方和等于斜邊的平方,即$BC^{2} + AC^{2} = AB^{2}$,所以C選項正確。
D. 在$Rt\triangle ABC$中,$\angle B = 90^{\circ}$,則$AC$是斜邊,應(yīng)該是$BC^{2} + AB^{2} = AC^{2}$,而不是$BC^{2} + AC^{2} = AB^{2}$,所以D選項錯誤。
1.某直角三角形的兩條邊長分別是3和5,那么第三條邊長的平方為
。
答案:$16$或$34$
解析:
本題可根據(jù)勾股定理,結(jié)合直角三角形兩條邊長分別是$3$和$5$,分情況討論第三條邊為斜邊或直角邊時的情況。
勾股定理是指直角三角形兩直角邊的平方和等于斜邊的平方。
情況一:當$5$是斜邊時
設(shè)另一條直角邊為$x$,根據(jù)勾股定理可得$x^{2}=5^{2}-3^{2}=25 - 9 = 16$。
情況二:當$5$和$3$都是直角邊時
設(shè)斜邊為$y$,根據(jù)勾股定理可得$y^{2}=3^{2}+5^{2}=9 + 25 = 34$。
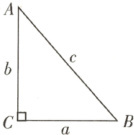
2. 如圖,在$\triangle ABC$中,已知$\angle C=90^{\circ}$,$a$,$b$,$c$是$\triangle ABC$的三邊長。
(1)若$c = 25$,$a = 7$,則$b =$
;
(2)若$c = 40$,$a:b = 3:4$,則$a =$
,$b =$
。
答案:24;24;32
解析:
(1)在Rt△ABC中,∠C=90°,由勾股定理得$a^2 + b^2 = c^2$。已知$c=25$,$a=7$,則$b = \sqrt{c^2 - a^2} = \sqrt{25^2 - 7^2} = \sqrt{625 - 49} = \sqrt{576} = 24$。
(2)設(shè)$a=3k$,$b=4k$($k>0$)。由勾股定理得$(3k)^2 + (4k)^2 = c^2$,即$9k^2 + 16k^2 = 40^2$,$25k^2 = 1600$,$k^2 = 64$,$k=8$。所以$a=3×8=24$,$b=4×8=32$。
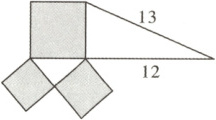
【例2】如圖所示的是由兩個直角三角形和三個正方形組成的圖形,其中陰影部分的面積是 (
)
A.50
B.16
C.25
D.41
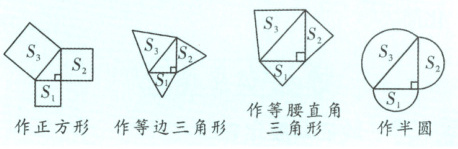
【方法點撥】巧用勾股定理求面積:以兩直角邊為邊長(或直徑)所作的兩個圖形的面積和等于以斜邊為邊長(或直徑)所作圖形的面積,即$S_{3}=S_{1}+S_{2}$。
答案:C
解析:
根據(jù)勾股定理,對應(yīng)面積關(guān)系為 $S_3 = S_1 + S_2$。
由圖示可知,直角三角形斜邊為 13,一個直角邊為 12。
根據(jù)勾股定理,另一條直角邊為:
$\sqrt{13^2 - 12^2} = \sqrt{169 - 144} = \sqrt{25} = 5$,
陰影部分對應(yīng) $S_2$,即邊長為 5 的正方形面積:
$S_2 = 5^2 = 25$。
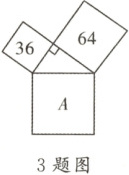
3. 如圖,三個正方形圍成一個直角三角形,圖中的數(shù)據(jù)是它們的面積,則正方形A的邊長為 (
)
A.6
B.8
C.10
D.12
答案:C
解析:
設(shè)直角三角形的兩條直角邊對應(yīng)的正方形面積分別為36和64,斜邊對應(yīng)的正方形面積為A的面積。根據(jù)勾股定理,直角三角形兩條直角邊的平方和等于斜邊的平方,即兩個小正方形的面積和等于大正方形的面積。所以正方形A的面積為36+64=100,其邊長為√100=10。
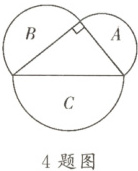
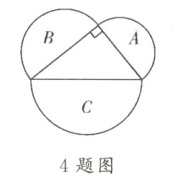
4. 如圖,以一個直角三角形的三邊為直徑向外作3個半圓。已知半圓A,B的直徑長分別是$a$,$b$,直角三角形的斜邊長為$c$。
(1)$S_{A}=$
;$S_{B}=$
;
(
2)
若$S_{A}=6$,$S_{B}=8$,
則$S_{C}=$
。
答案:$\frac{\pi a^{2}}{8}$;$\frac{\pi b^{2}}{8}$;14
解析:
(1) 半圓A的直徑為a,半徑為$\frac{a}{2}$,面積$S_{A}=\frac{1}{2}\pi(\frac{a}{2})^{2}=\frac{\pi a^{2}}{8}$;半圓B的直徑為b,半徑為$\frac{b}{2}$,面積$S_{B}=\frac{1}{2}\pi(\frac{b}{2})^{2}=\frac{\pi b^{2}}{8}$。
(2) 由勾股定理得$a^{2}+b^{2}=c^{2}$。半圓C的直徑為c,半徑為$\frac{c}{2}$,面積$S_{C}=\frac{1}{2}\pi(\frac{c}{2})^{2}=\frac{\pi c^{2}}{8}$。因為$S_{A}+S_{B}=\frac{\pi a^{2}}{8}+\frac{\pi b^{2}}{8}=\frac{\pi(a^{2}+b^{2})}{8}=\frac{\pi c^{2}}{8}=S_{C}$,所以$S_{C}=6+8=14$。






